線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
ブリタニカ国際大百科事典 小項目事典 点対称の用語解説 空間の1点oがある。oを通る線分上の2点p,qがoを中心として対応する位置にあるとき,この2点は点oに対して点対称であるという。また,1つの図形が,oに関する2直角の回転移動によって自分自身に重ね合せられるとき,この図形は平均値は (30+35+40+40+90)÷5=47 点 となり、 90 点以外の4人は平均値以下 です。 中央値は、真ん中の値ですので 40 点 となります。 このように、 平均値の場合は他の値と比べて極端に高い(もしくは低い)値があることによって、影響を受けてしまい
点対称とは 簡単に
点対称とは 簡単に- スポンサーリンク 数学点の「対称移動(たいしょういどう)ってどうやるの? 高校数学 数学おじさん 点の対称移動を理解するには、 次の3つの点を理解するといいんじゃ ①、X軸対称 ②、Y軸対称 ③、原点対称直線に関して対称な点の求め方 ポイント 点と直線の距離の公式 ポイント 放物線と直線の共有点の求め方 ポイント 直線と放物線の共有点の分類 会員登録をクリックまたはタップすると、 利用規約・プライバシーポリシー に同意したものとみなします
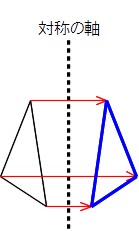
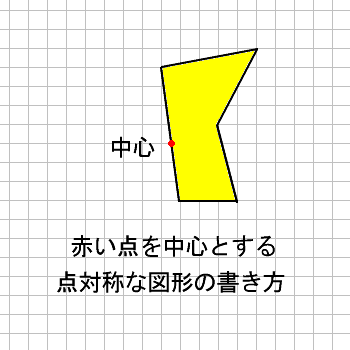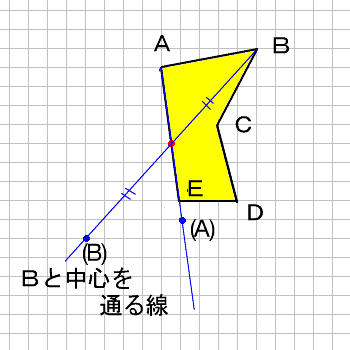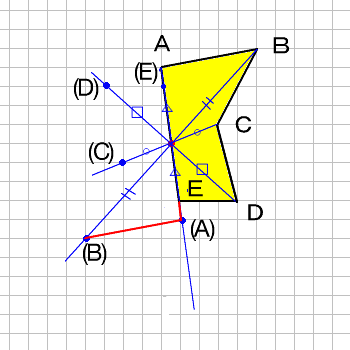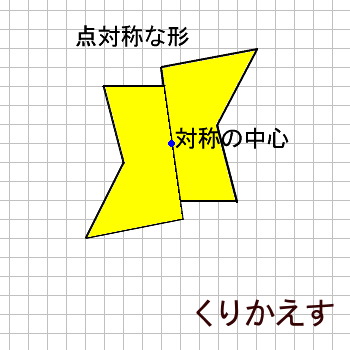
Math 点対称な図形のかき方 働きアリ
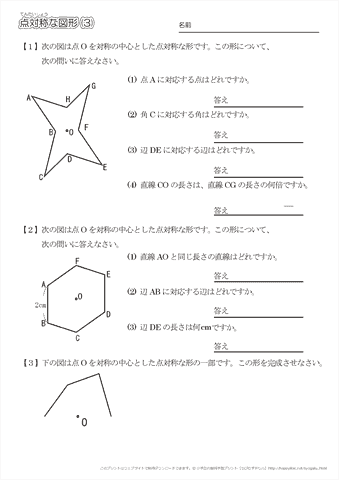
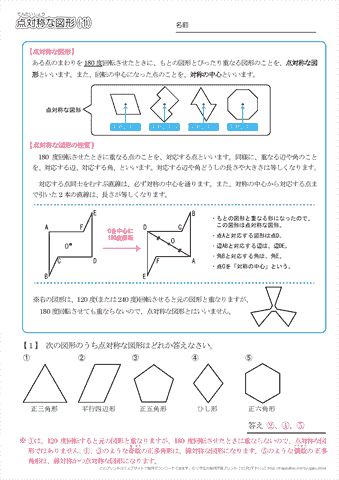
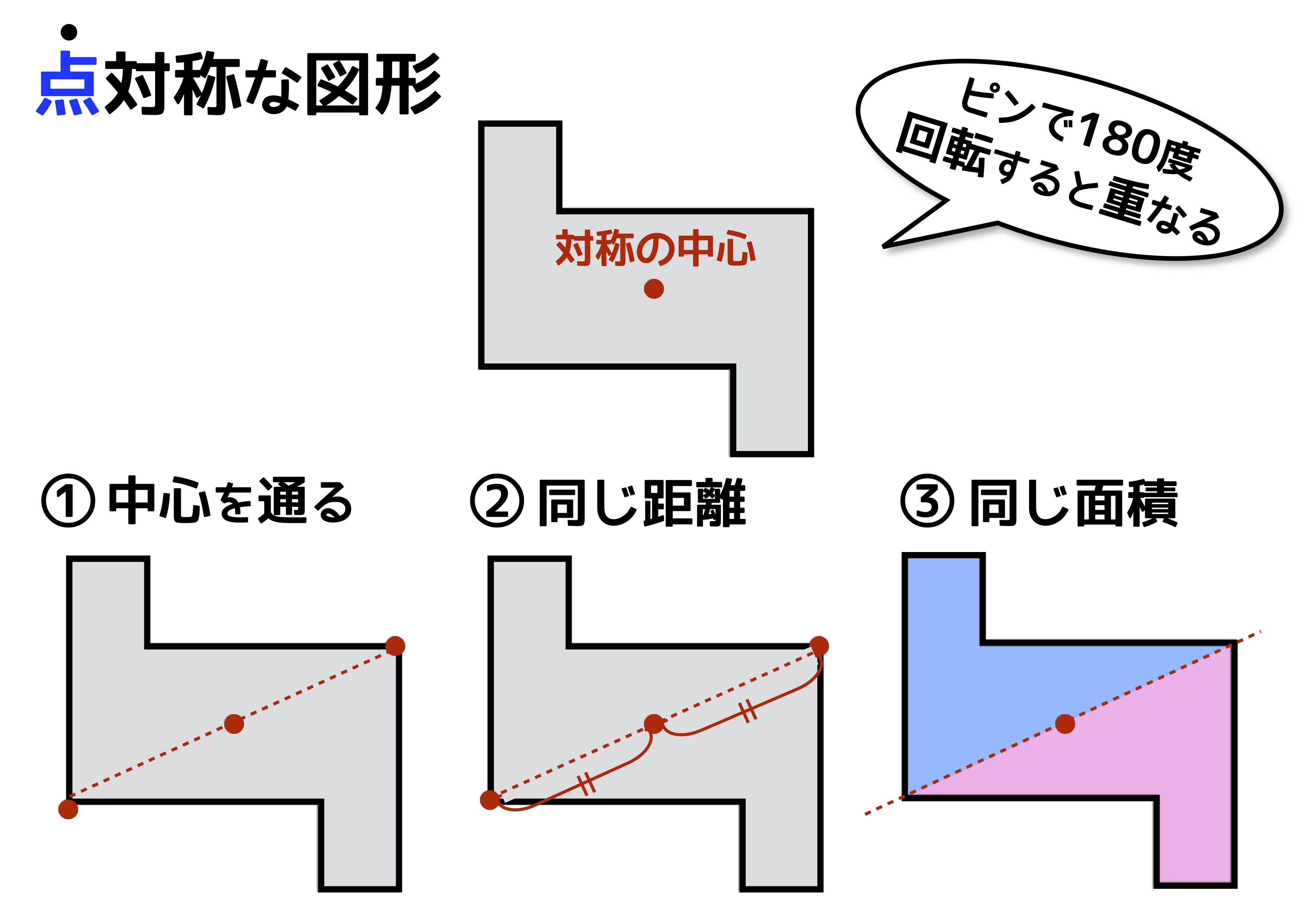
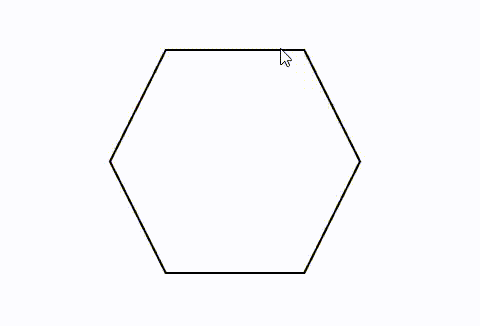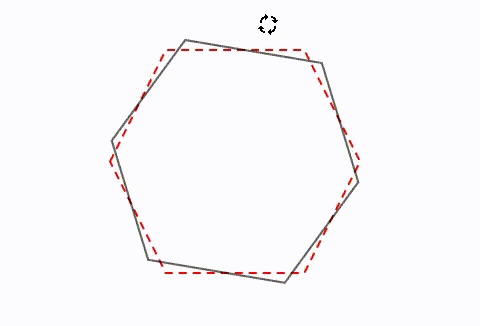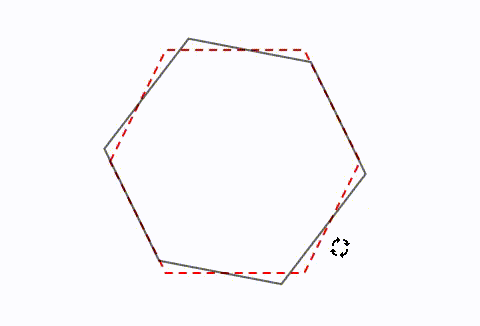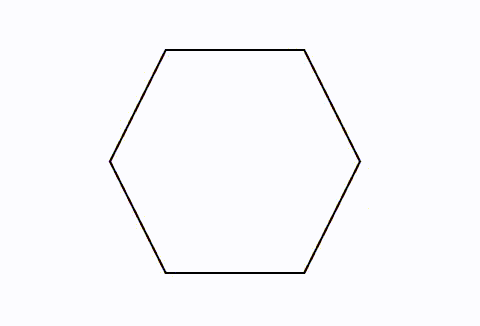
正規分布(ガウス分布)とは簡単にいうとどんな分布?なぜ重要なの? 正規分布(又の名を"ガウス分布" )は、下の図のような形をしています。 この形が鐘の形に似ているため、正規分布が描く曲線のことをベルカーブとも呼びます。すなわち、結晶の任意の性質が示す対称性は、結晶の点群の対称性よりも低くはなりえないのである。 これをノイマンの原理(Neumann's Principle)と呼ぶ。 ある系の対称性を考えるには、ある操作を行う前後で変化があるかないかを考えることになる。点対称な図形 解説 次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を 点対称な図形 といいます。 このとき回転の中心となる点を 対称の中心 といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な
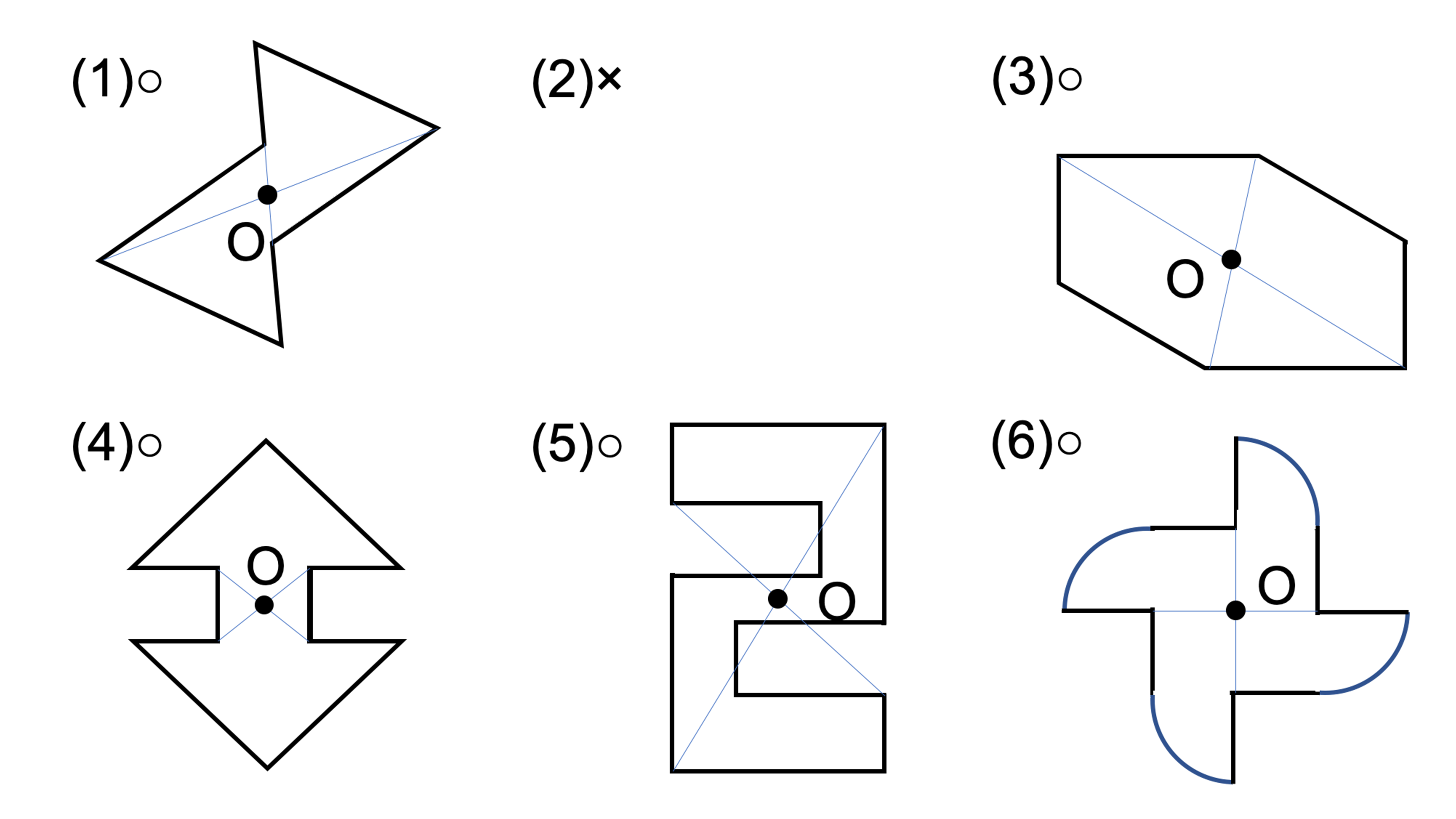
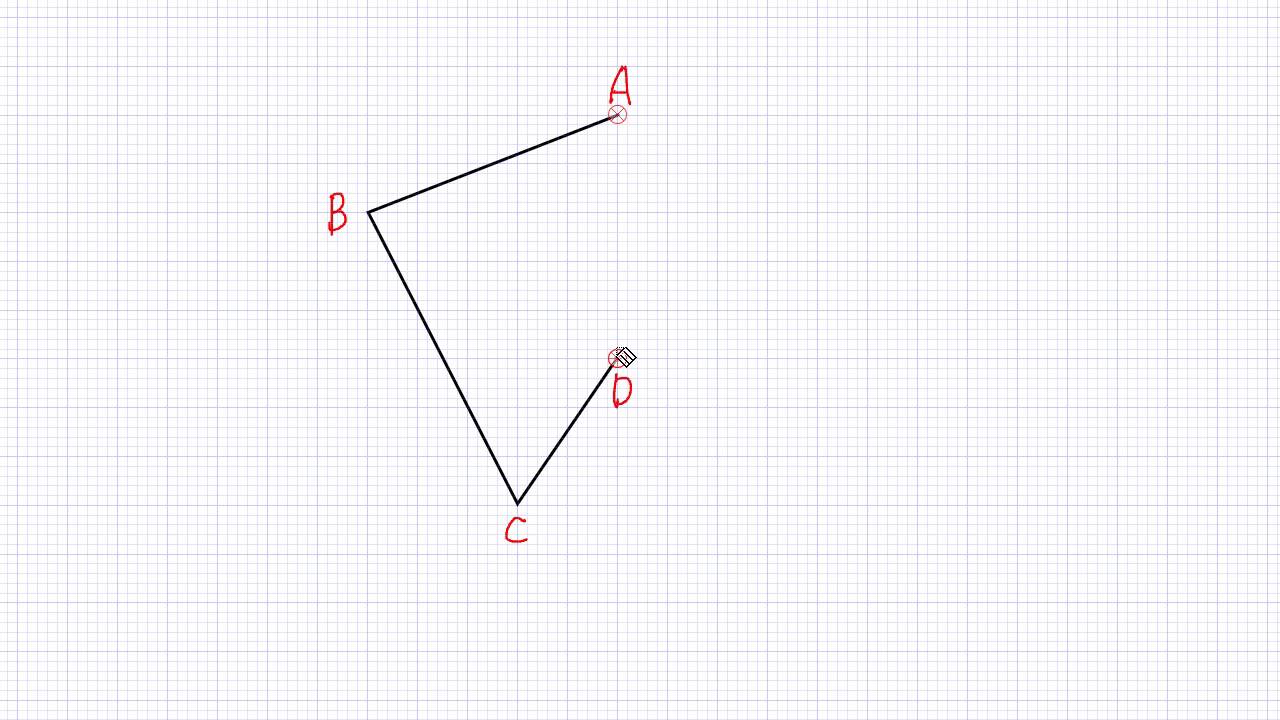
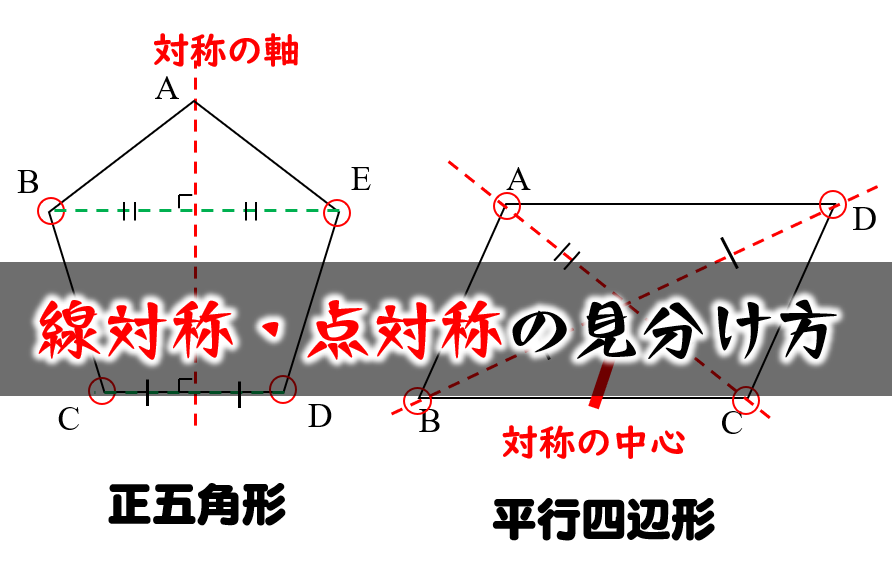
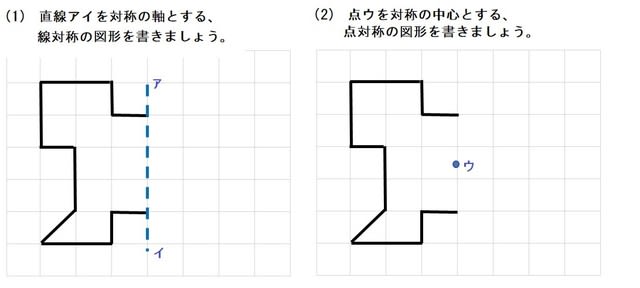
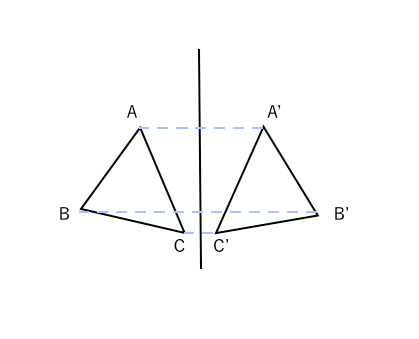
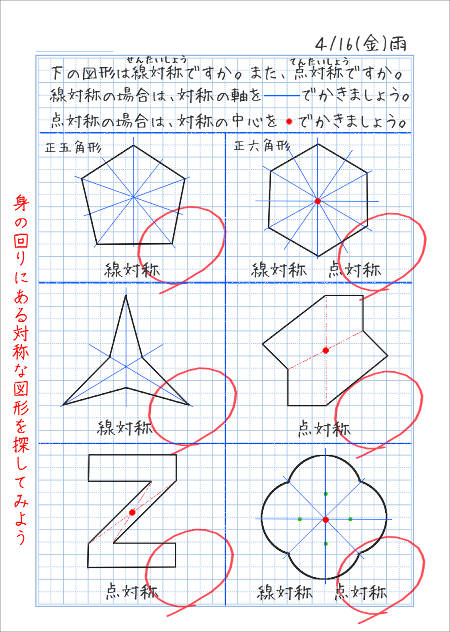
線対称や点対称を見つける問題です。 線対称は折ったときに重なるか、点対称は180度回したときに重なるかです。 対称の軸の本数もここで学習します。 78・3 対称な図形の作図の練習です。 それほど簡単ではありません。 慎重に根気よくかいていきます 方べきの定理とは,円と点 p p p と2 昔の東大入試では簡単な問題も出題されている。 この記事では,図形やグラフの移動の代表例である 線対称移動,点対称移動 に まず、対称であることから、直線 l と A との距離と、直線 l と B との距離は同じです。 ただ、点と直線との距離を求めるのは大変です。それよりも、もっとシンプルに「 AB の中点が、直線 l の上にある 」と考えたほうが、計算は簡単になります。
点対称とは 簡単にのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
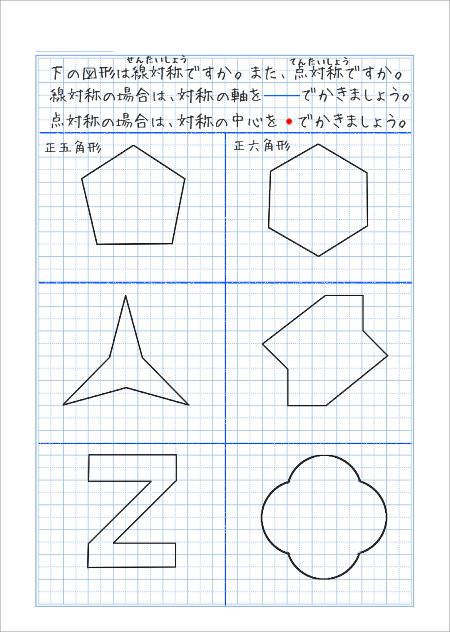
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 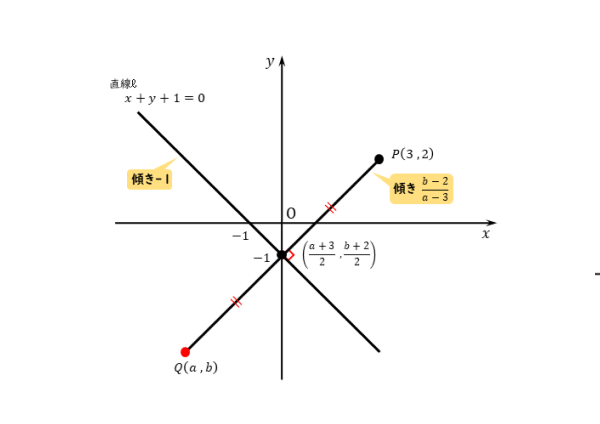 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 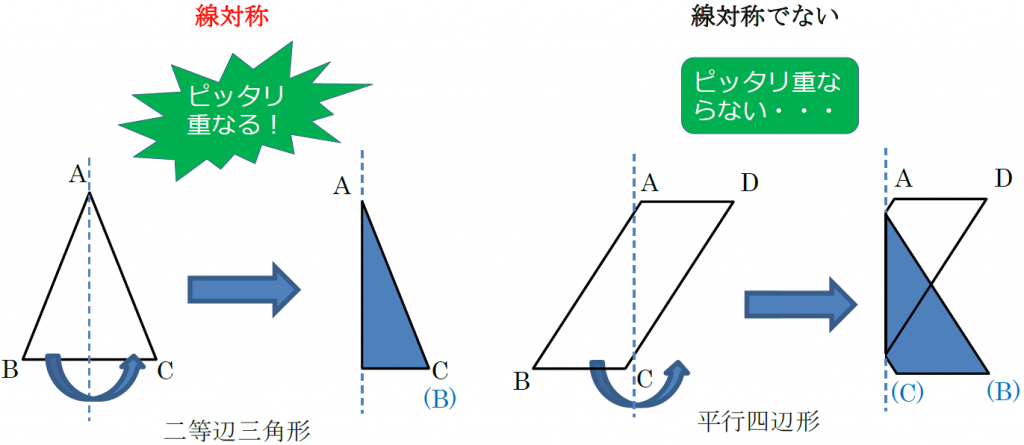 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 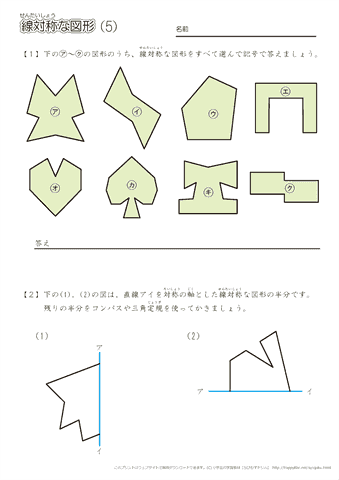 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 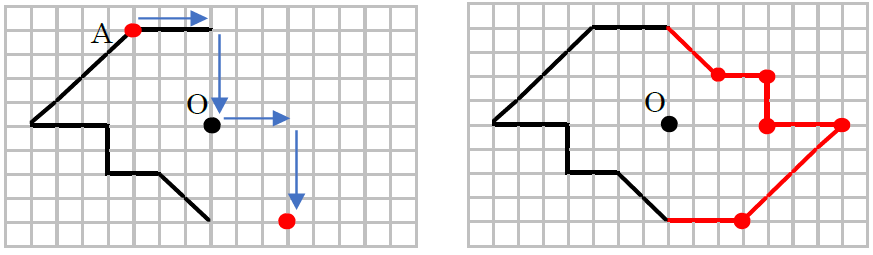 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 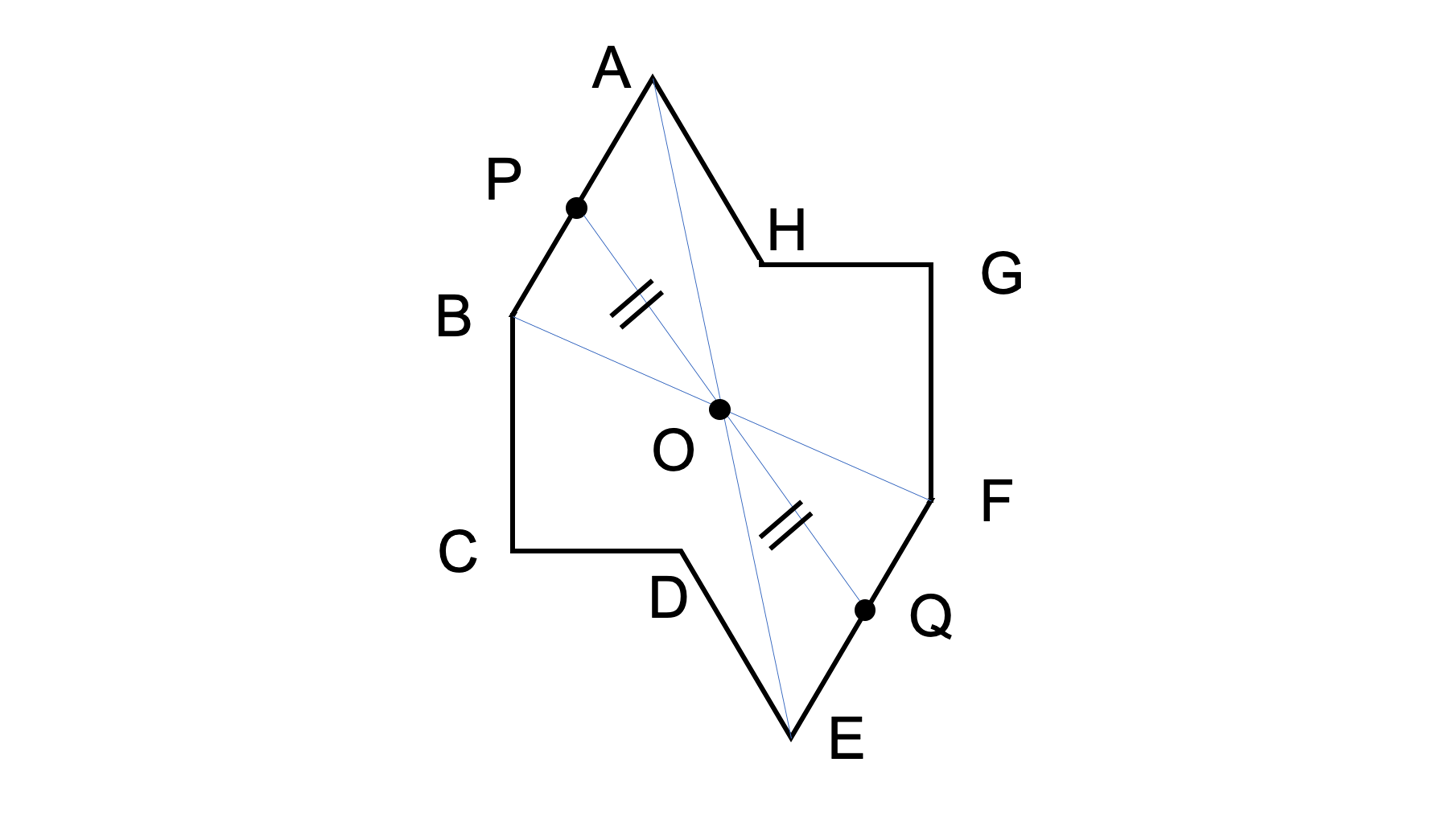 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 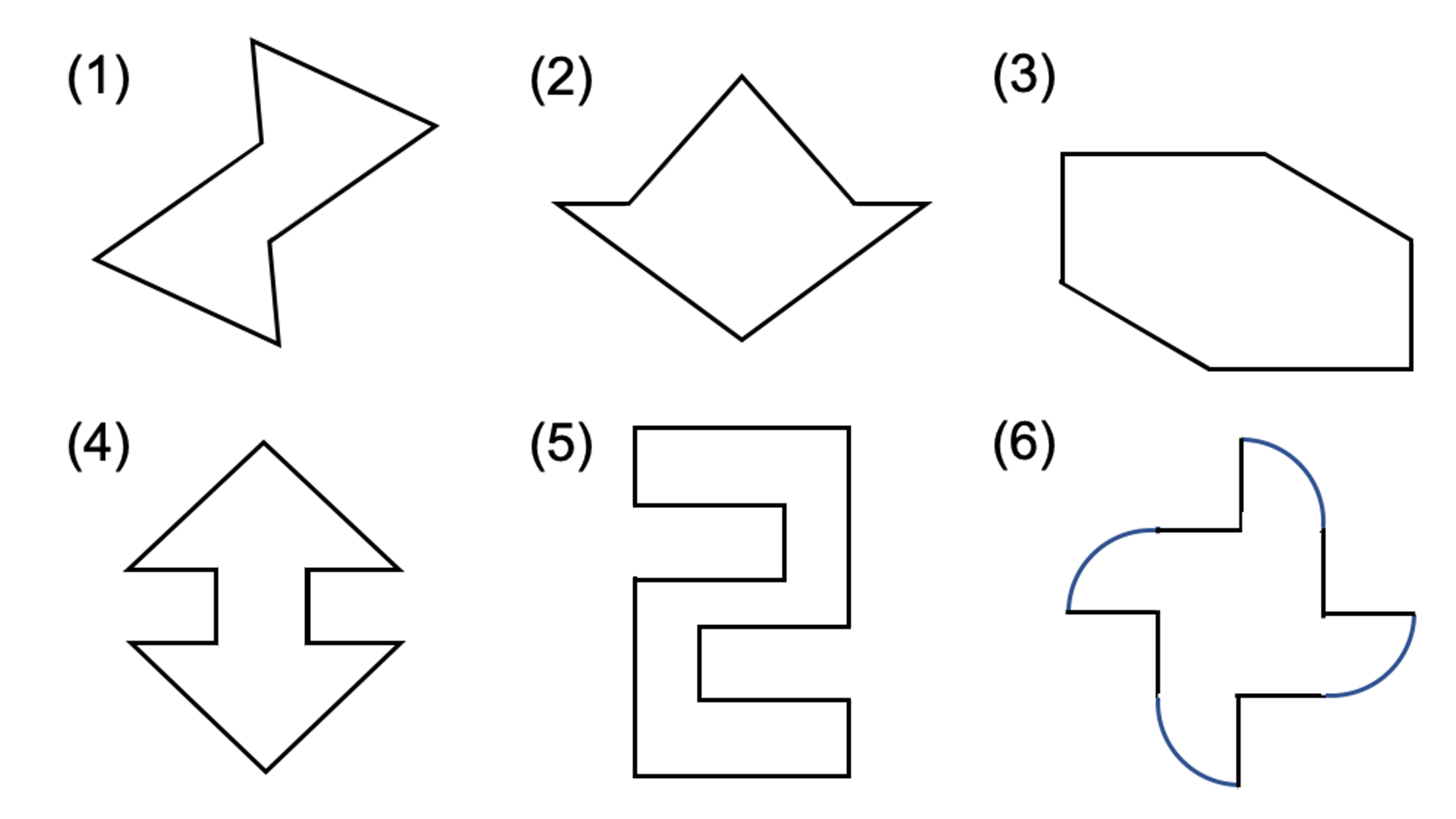 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 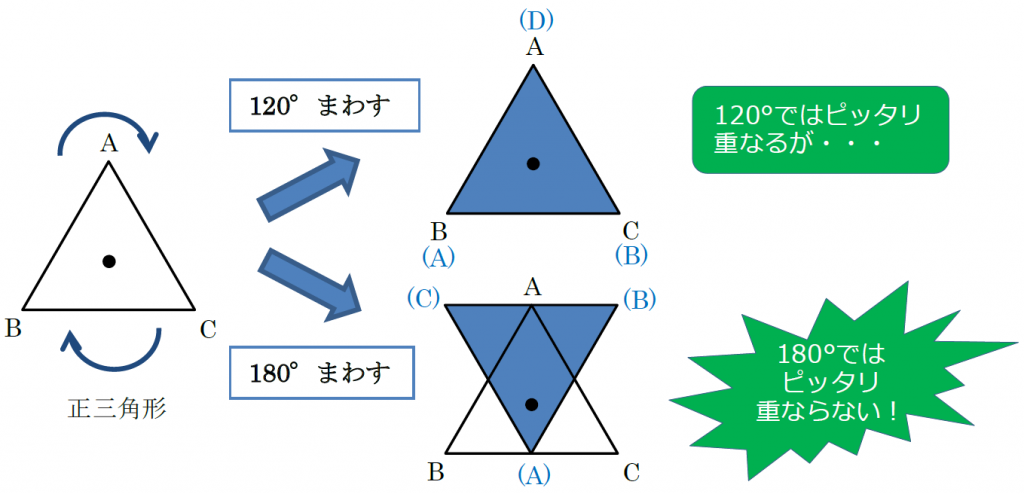 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 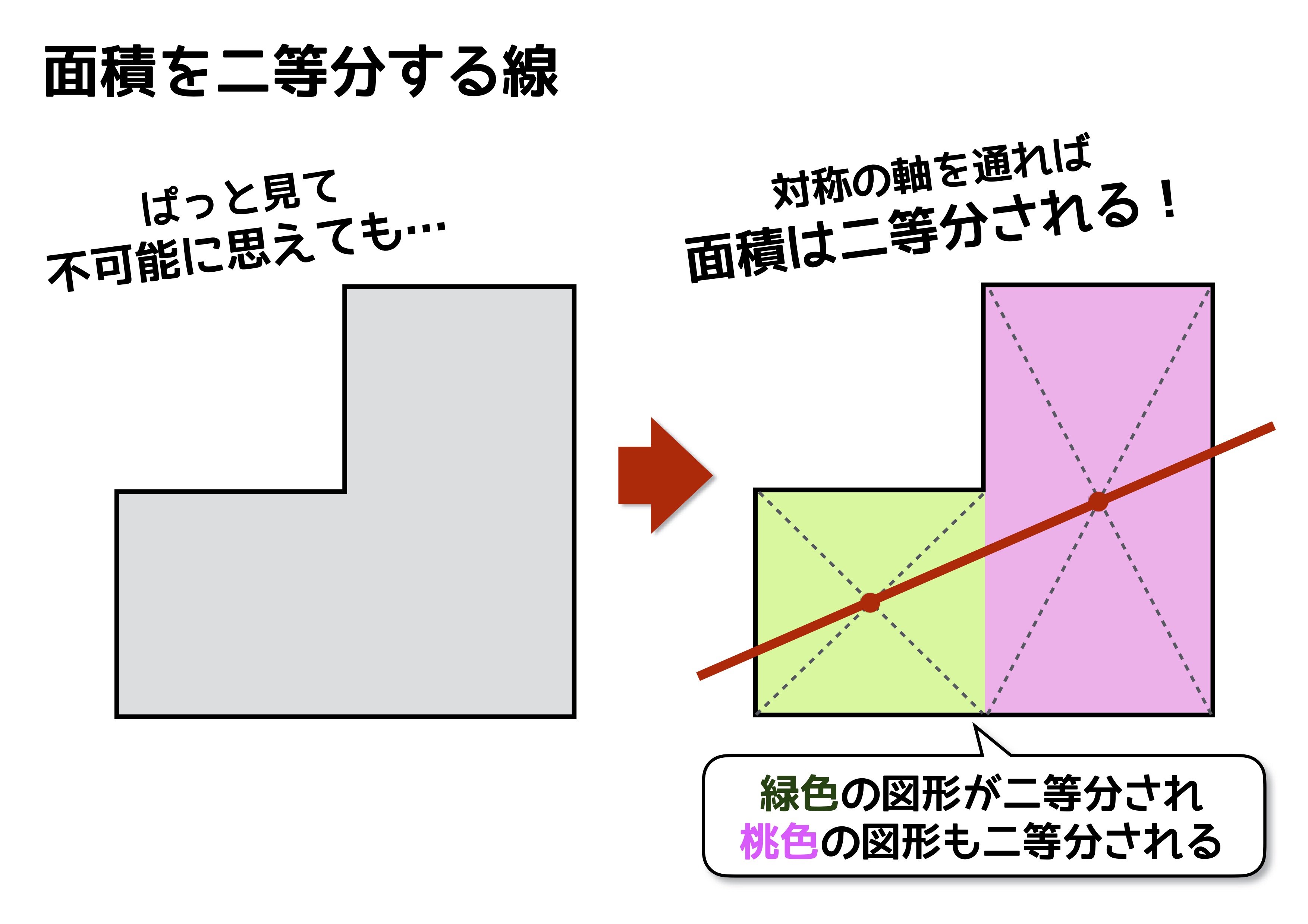 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 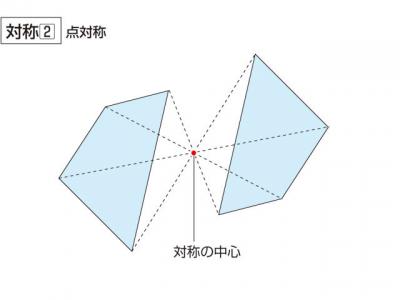 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 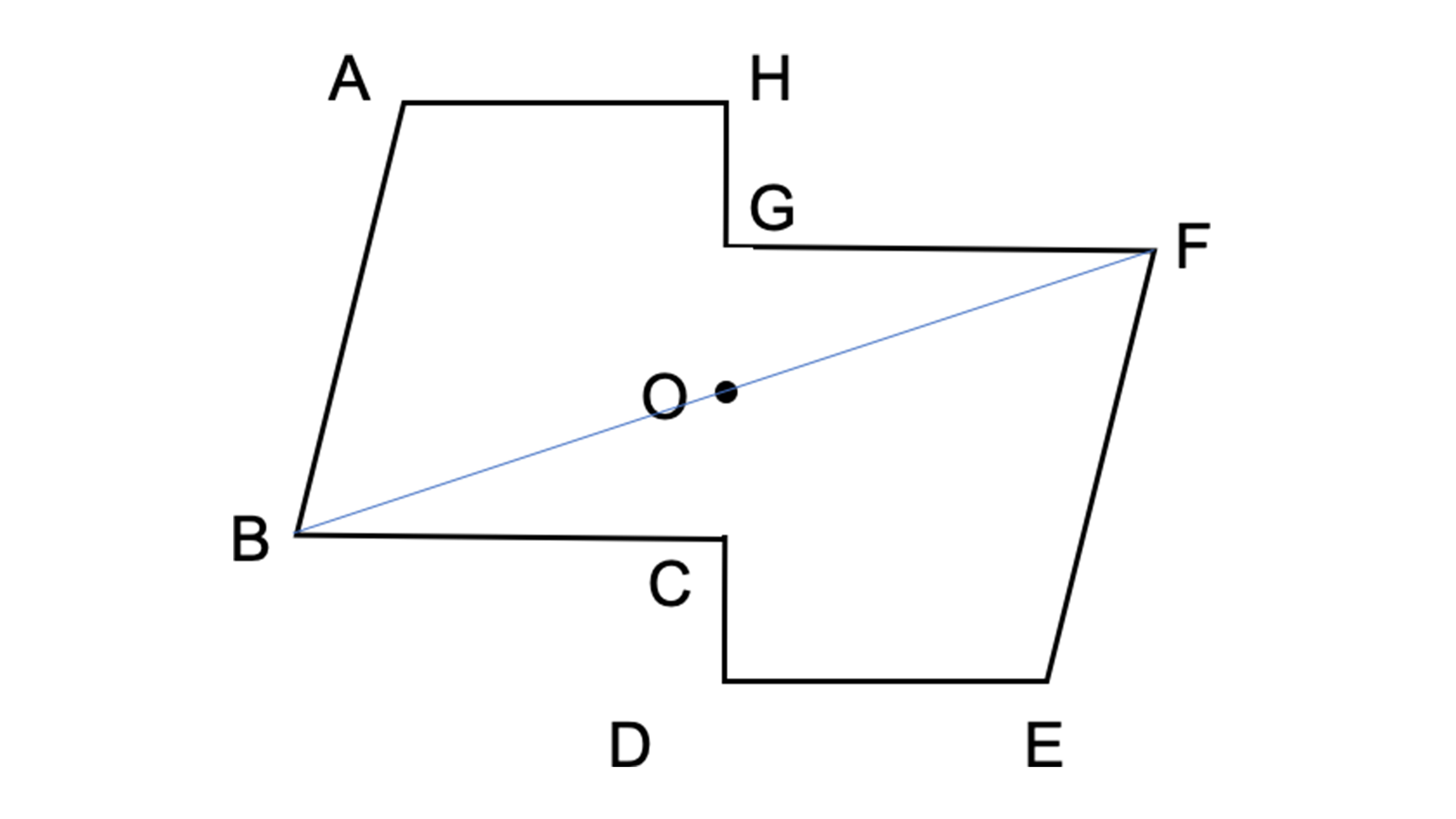 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 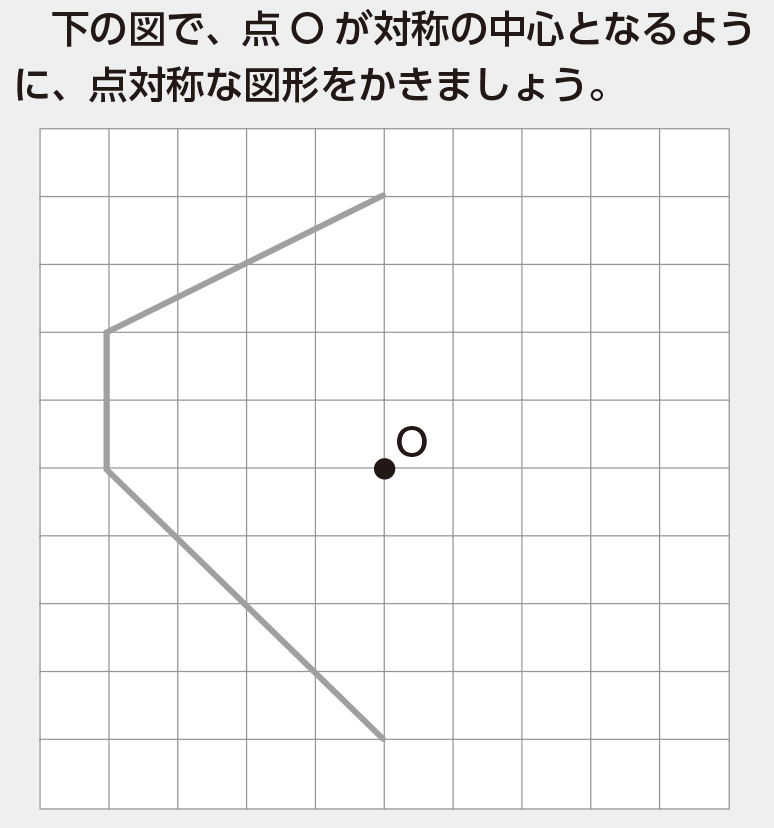 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 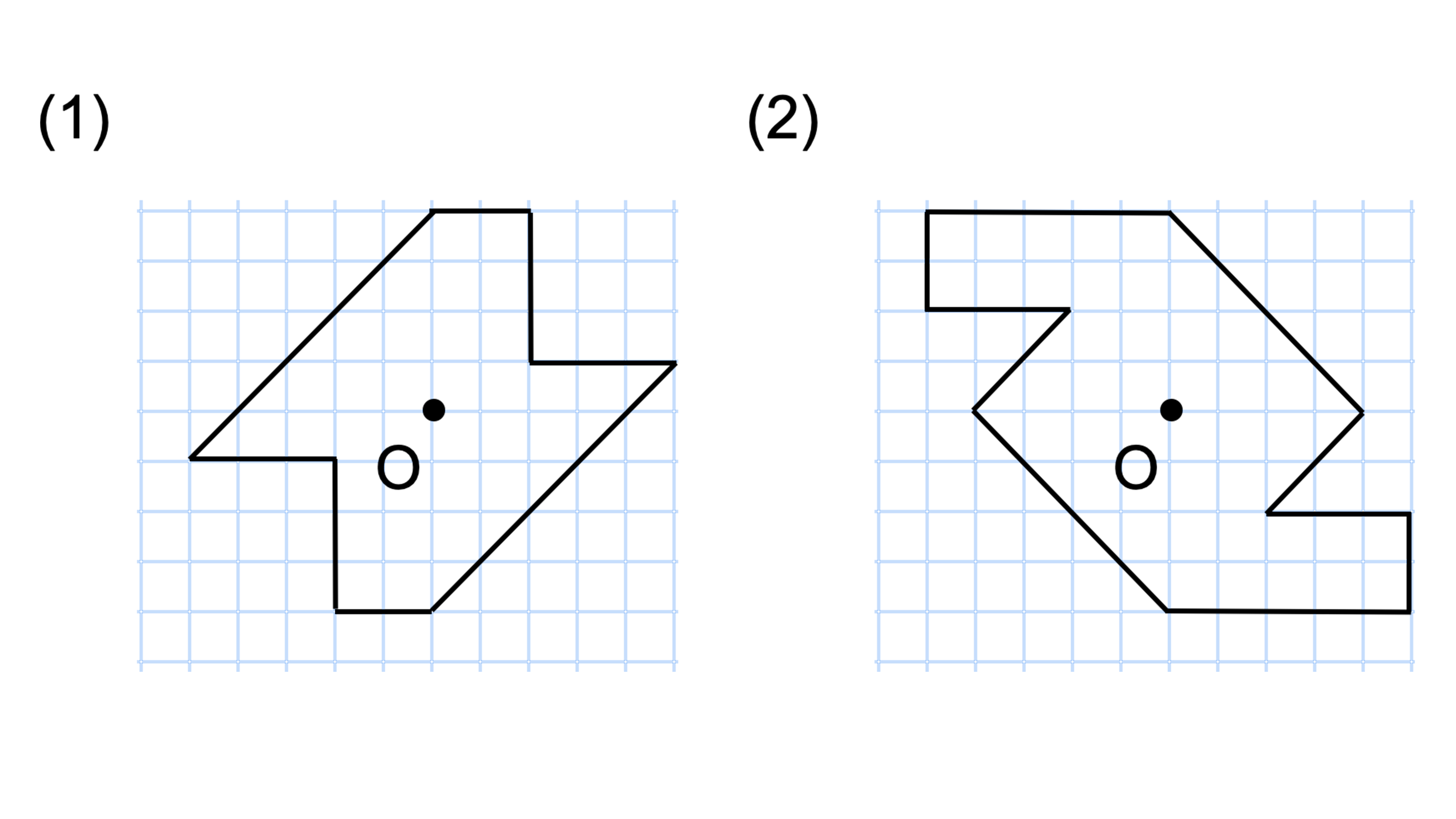 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 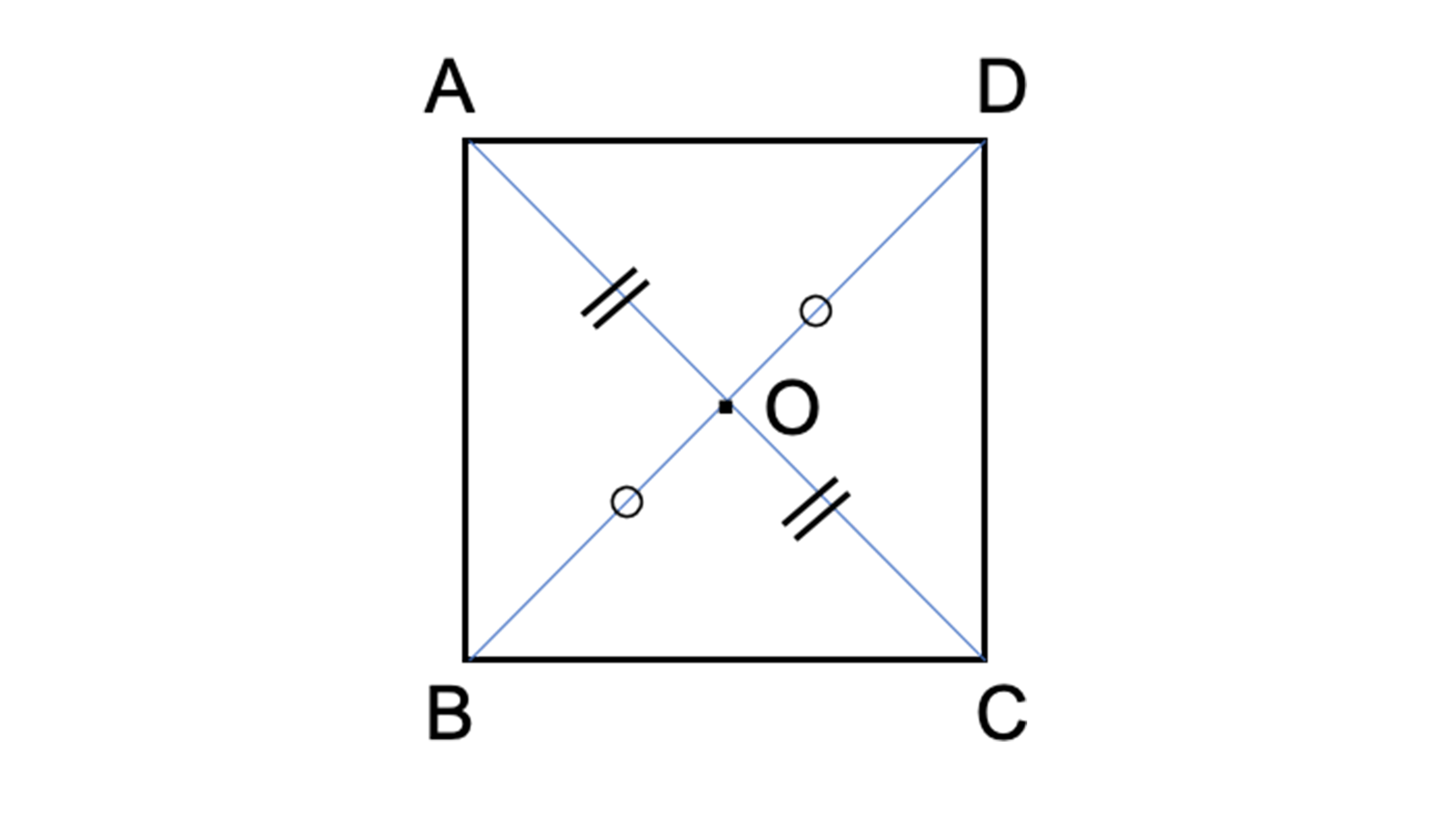 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 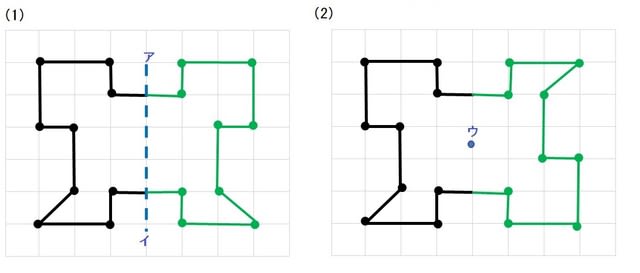 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 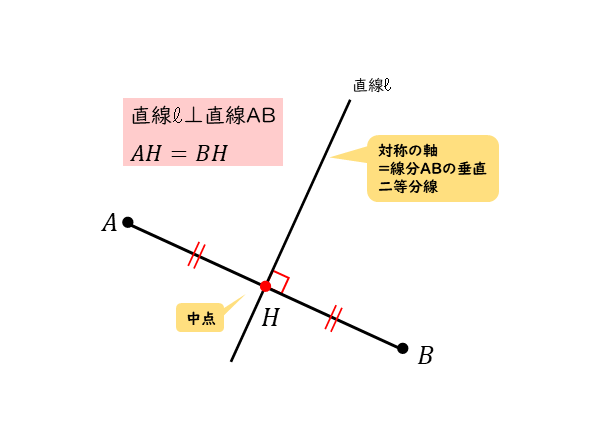 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 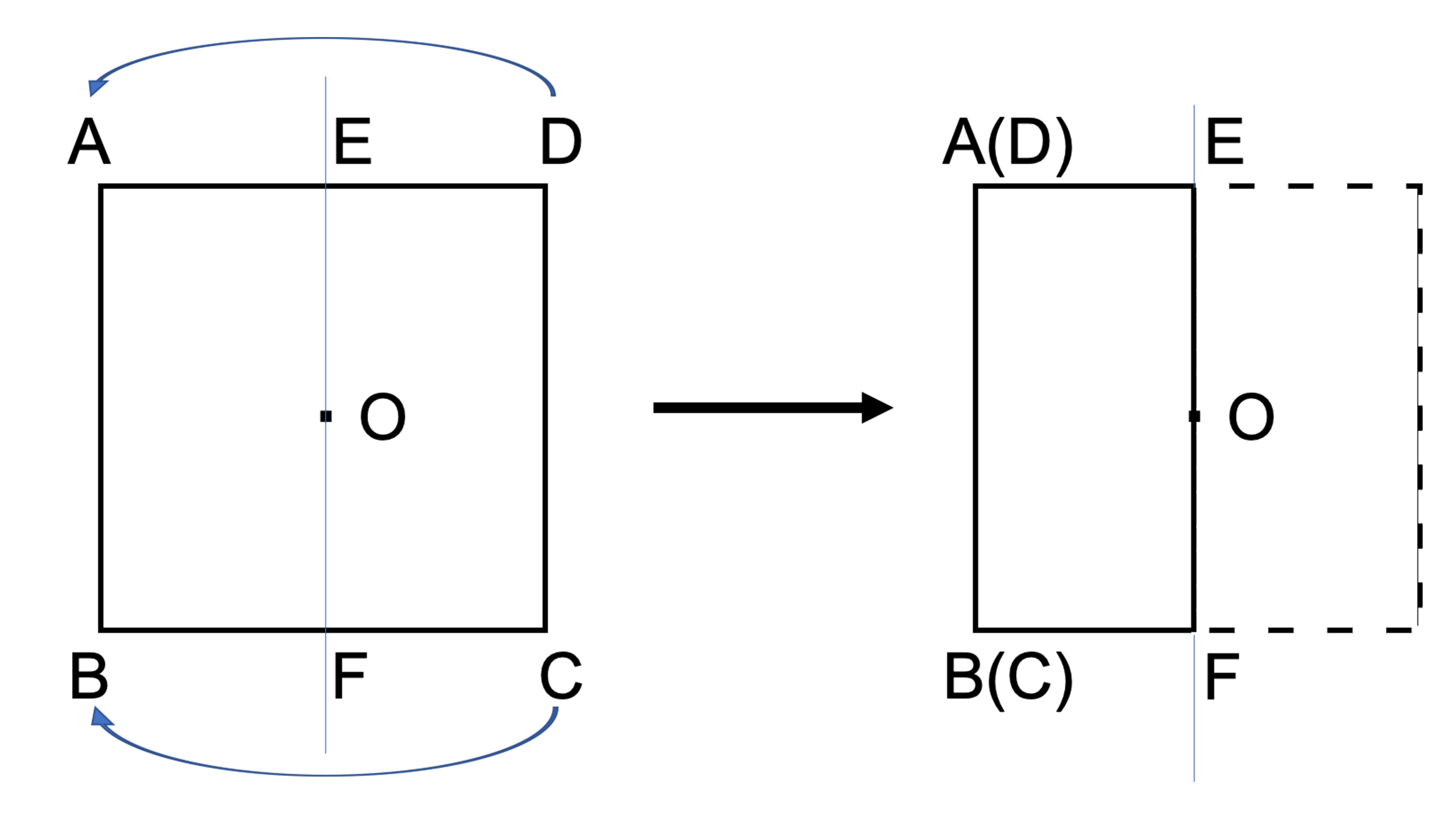 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 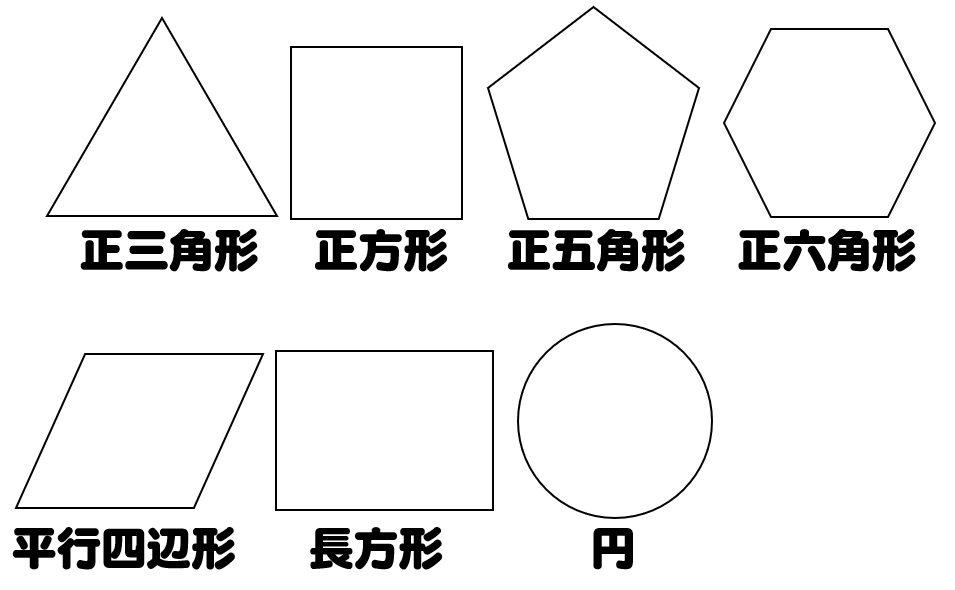 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 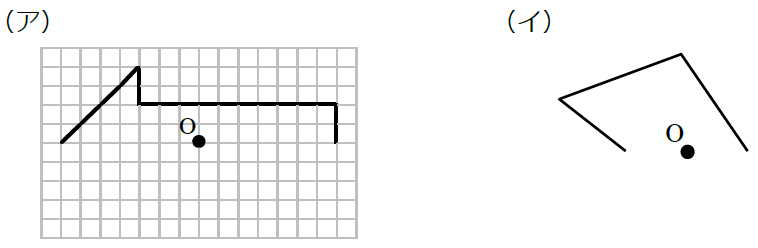 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 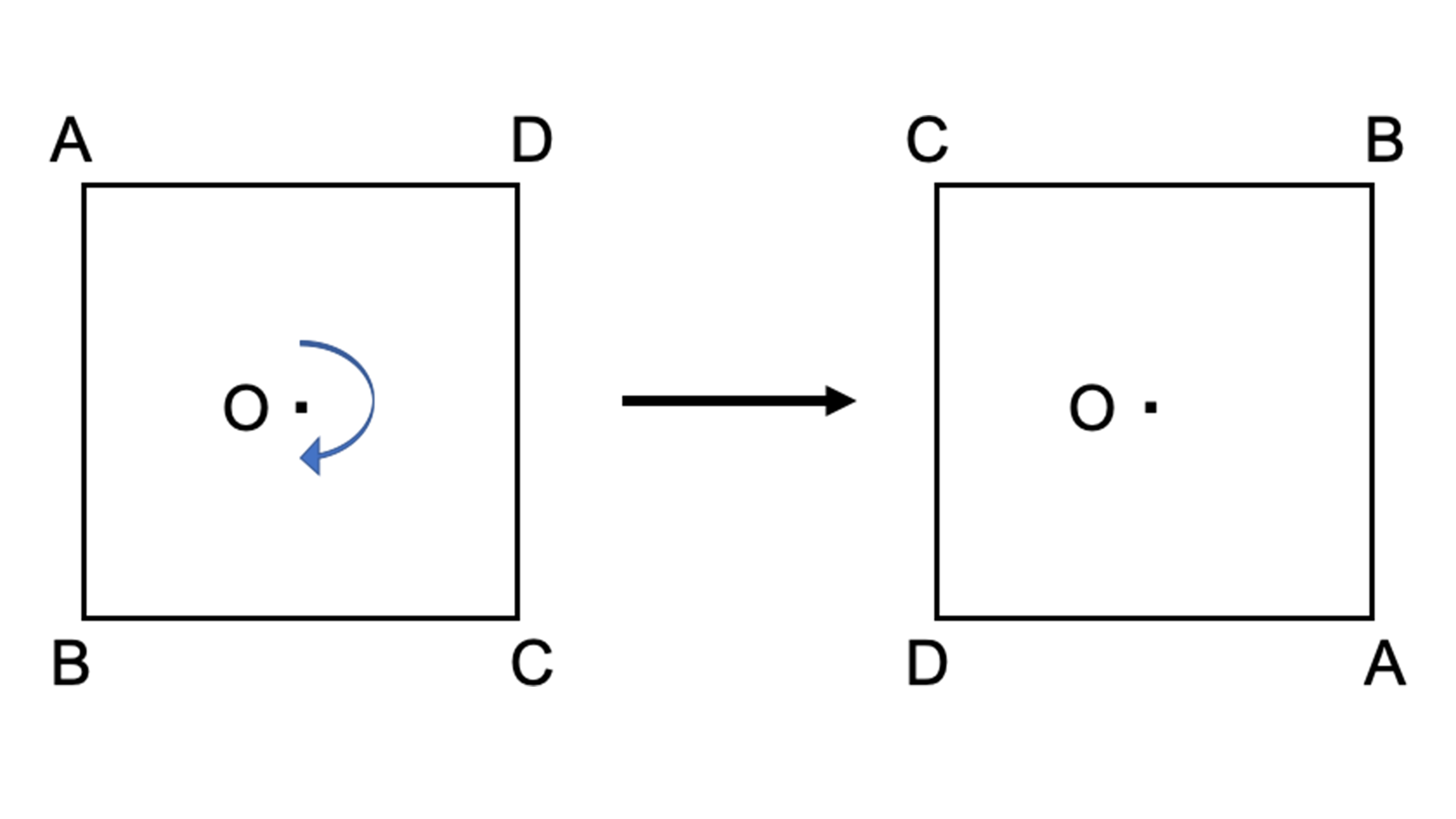 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 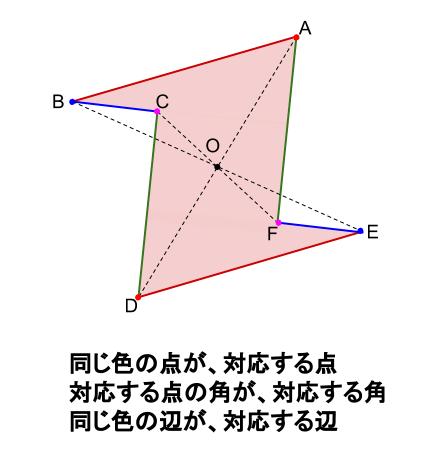 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 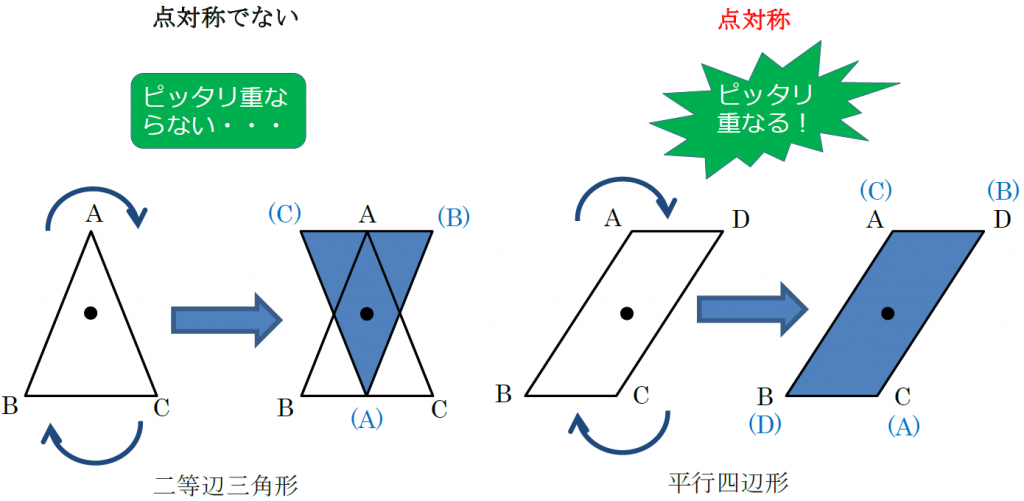 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
「点対称とは 簡単に」の画像ギャラリー、詳細は各画像をクリックしてください。
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 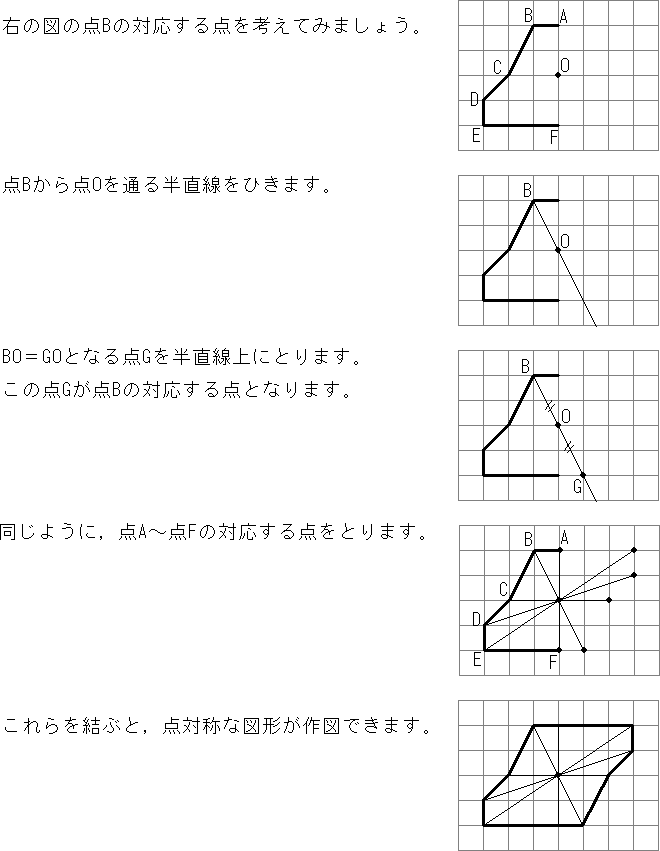 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |  小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 | 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生 |
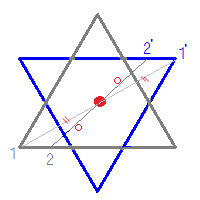
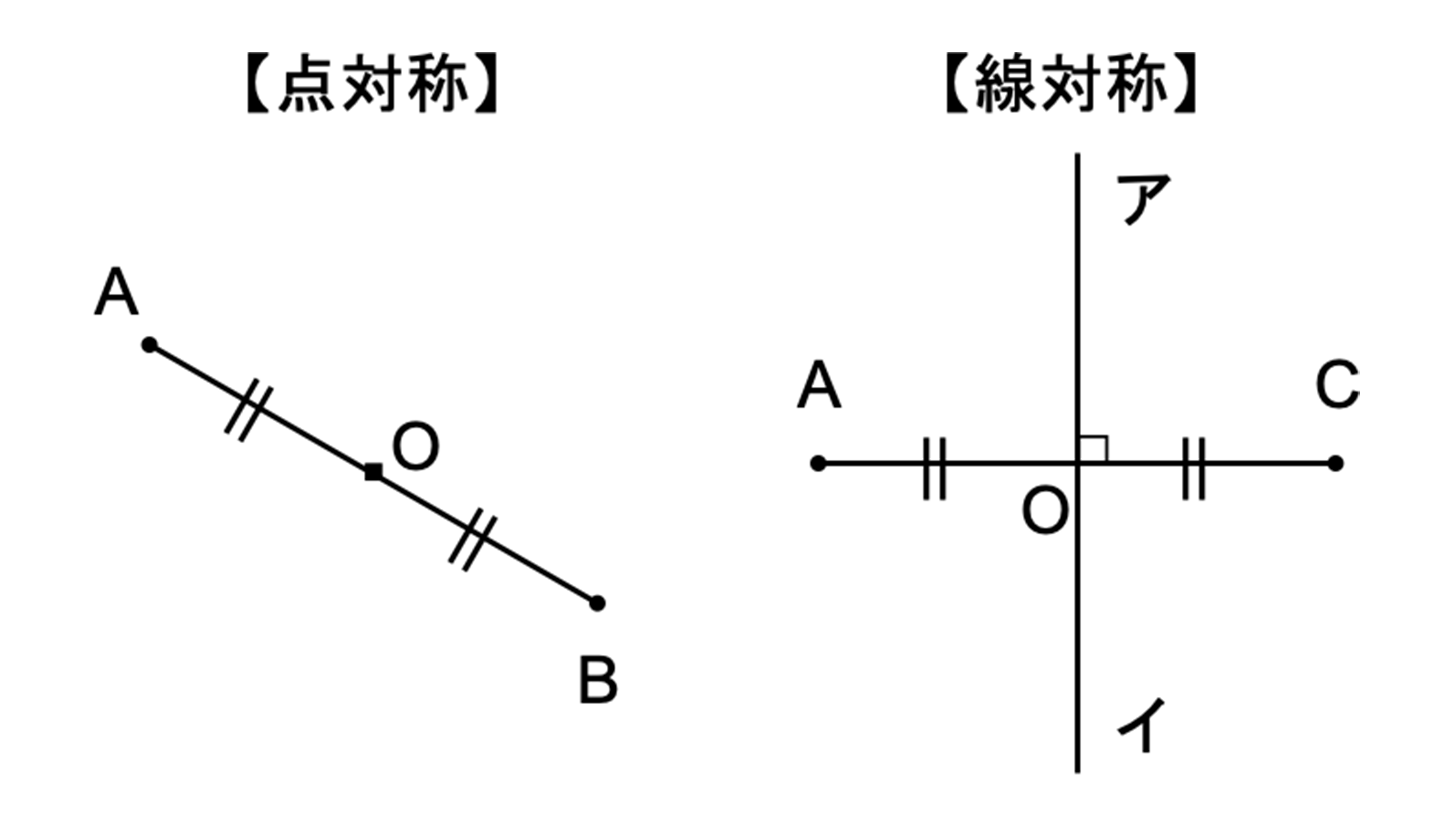
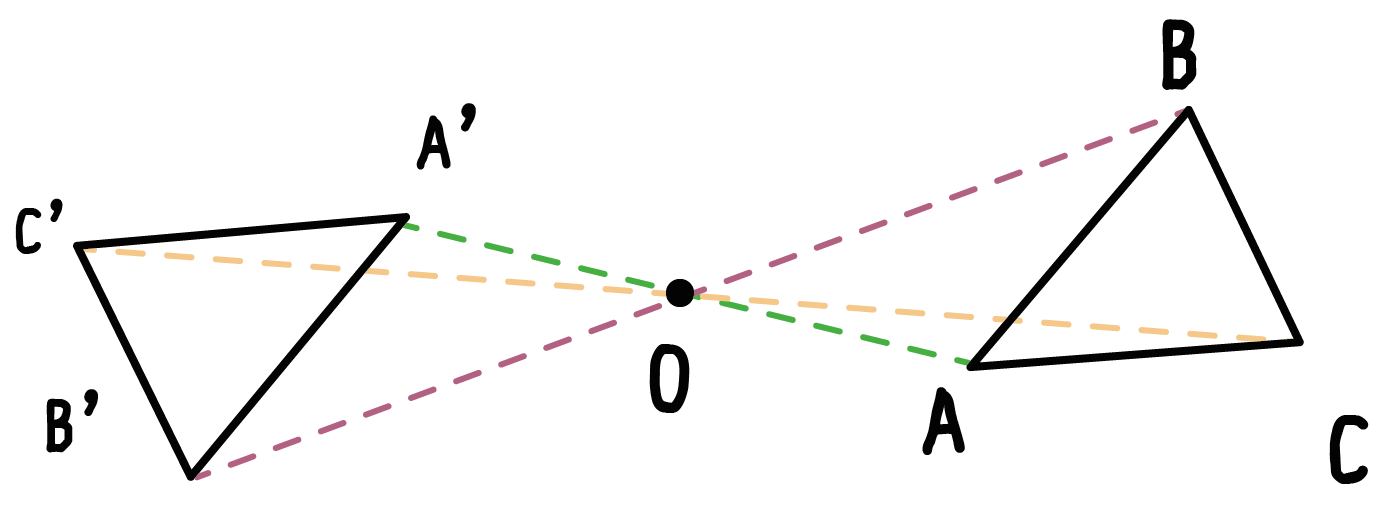
点対称において、回転させる中心となる点を 「対称の中心」 と言い、対称の中心を軸に180°回転させて重なる点や辺を「対応する点」や「対応する辺」と言います。 この平行四辺形の場合、「点a」に対応する点は「点c」、「辺ab」に対応する辺は「辺cd」です。それぞれの点に対応する点があります。 ※ 花火のように広がる図形・放射状図形は,点対称と間違わないように気をつけましょう。右の図は点対称な図形ではありません。 180°回転しても元の図形と一
Incoming Term: 点対称とは 簡単に,




0 件のコメント:
コメントを投稿