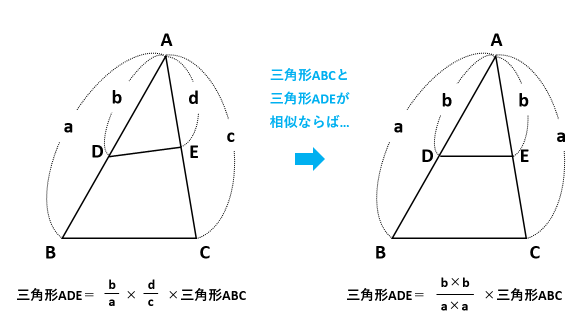
オリフィスノズルの絞り面積比crが オリフィス噴流の 流動特性に及ぼす影響を実験的に検討した結果,(1)流 れ の可視化画像からオリフィス噴流では周期的な大規模渦 が放出され,その大きさはcrが小さいほど大きくcrは渦 構造の形成に大きく関係する,(2)crが 小さいほど縮流 の程度が大きく,中心 ひたすら面積比のことだけ考え、脳内の"面積比濃度"を上げる。 面積比を克服するには、そんなトレーニングが必要です。 2つ目は、そもそも"型"がまとまっていない、ということ。 面積比を解くための"型"は、教える先生によってまとめ方が異なり 面積比の求め方といっしょ。 つまり、 相似比の2乗の比 になってるのよ。 相似比が12の「円錐A・Bの表面積の比」は、 1^2 2^2 = 1 4 になるわけね。 もし、円錐Bの表面積が40 cm^2だったら、 円錐Aの表面積は10 cm^2 になるわけだね。 おめでとう! 相似比

大至急です 相似 面積比の問題です Clear
面積の比とは
面積の比とは-5)プロペラの面積比 上記の通りプロペラの面積の測り方にはいろいろあるが実用上これらの面積をプロペラの全円面積で割った比で表わしておくと便利であるので、通常つぎのように表わしている。 (1)投影面積比 投影面積をプロペラの全円面積で割った値である。 (2)伸張面積比 伸張面積比の求め方を理解しよう こちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。




面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底 面積比の基本的な問題です。 応用問題に入る前に、このレベルの問題を確実に出来るようにしておきましょう。 ポイント 高さの等しい三角形は、底辺の比が面積比になる→図の中で高さの等しい三角形をすぐに見つける練習をしましょ場合③:鋼より銅の面積が圧倒的に多い場合,面積比 1:9 と仮定した時の鋼の腐食量を求める。 異種金属の面積比の影響 第一に,腐食速度は,酸素拡散律速なので,面積が同じ場合の酸素消費量は同じ量となる。このことは,酸素の還元に使われる電子の量も同じことを意味する。 第二に
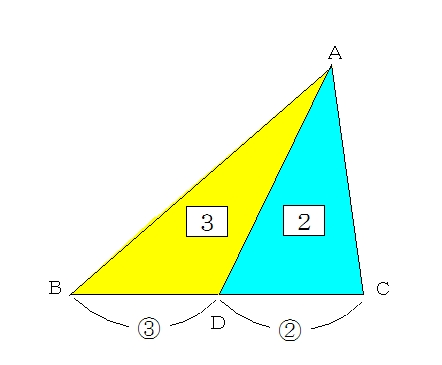
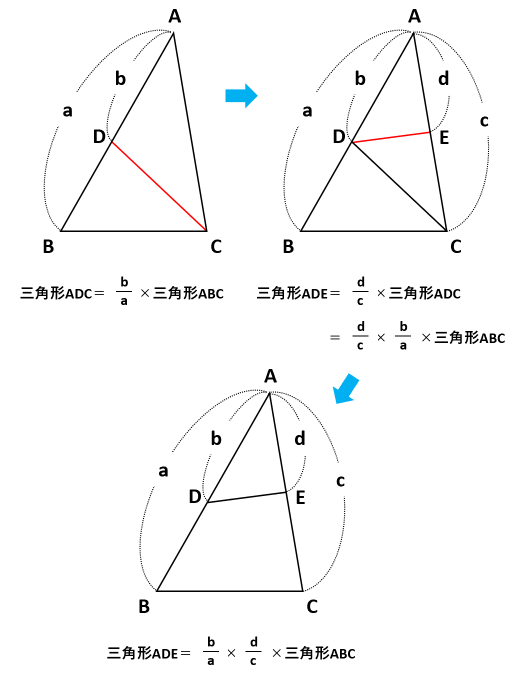
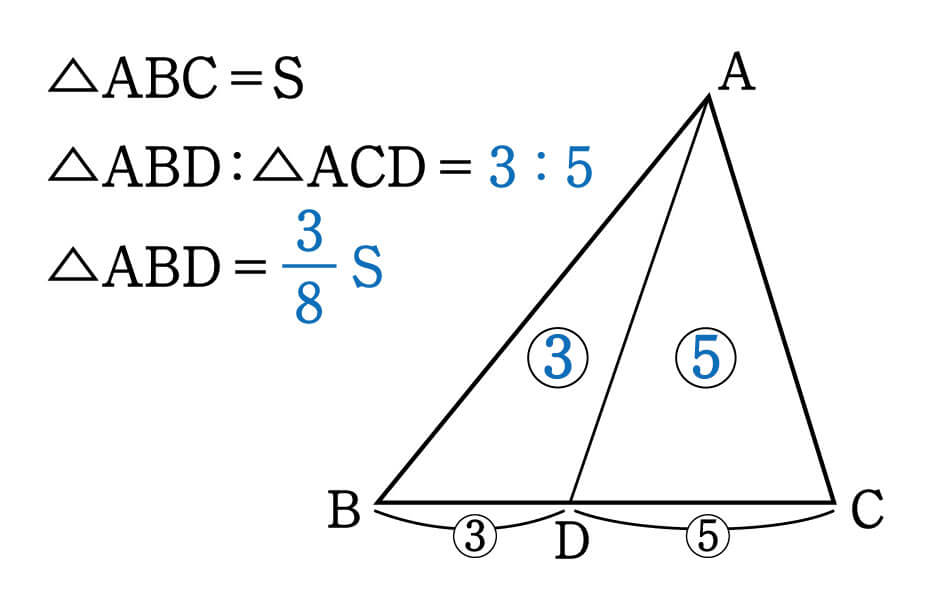
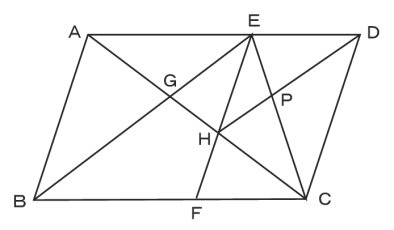
「辺の比と面積比」の基本は、なんと言っても下図です。 三角形ABD と 三角形ACD の面積の比は、 BDとDCの比に等しくなります。 問題に出されている図の中に、この基本パターンを見つけ出したり、 この基本パターンを当てはめるためには、どこに補助線を引いたら いいのか、を考えると、より三角形IGHの面積の比は49:9。よって、 三角形IGHの面積は9cm 2 。 解答:9cm 2 34. 右の図は面積が360cm 2 の正六角形で、G、H、Iは AB、BC、EFの中点です。 黄緑の部分の面積は何cm 2 ですか。 解説: 右の図のように正六角形を24個に分けると、 求める面積は17個分になる。 360÷24×17=255cm 2 。 解答 (1)は線分比が面積比になる性質を使いますが、2回使います。 (2)は線分比が面積比になる性質と相似比が面積比になる性質を使います。 このようなに複数回の比をとるときは整数比を調整します。 それはどういうことか? ab=23 cd=34 ac=45
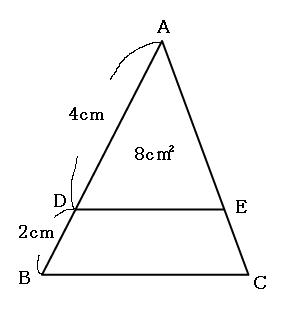
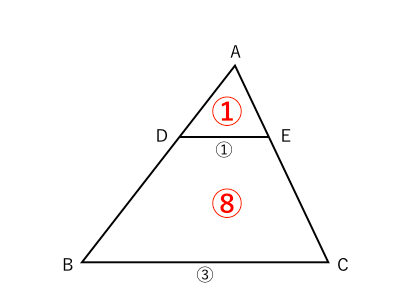
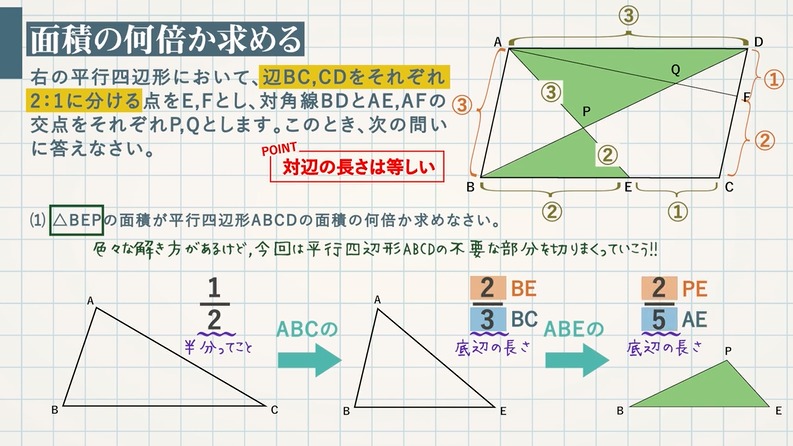
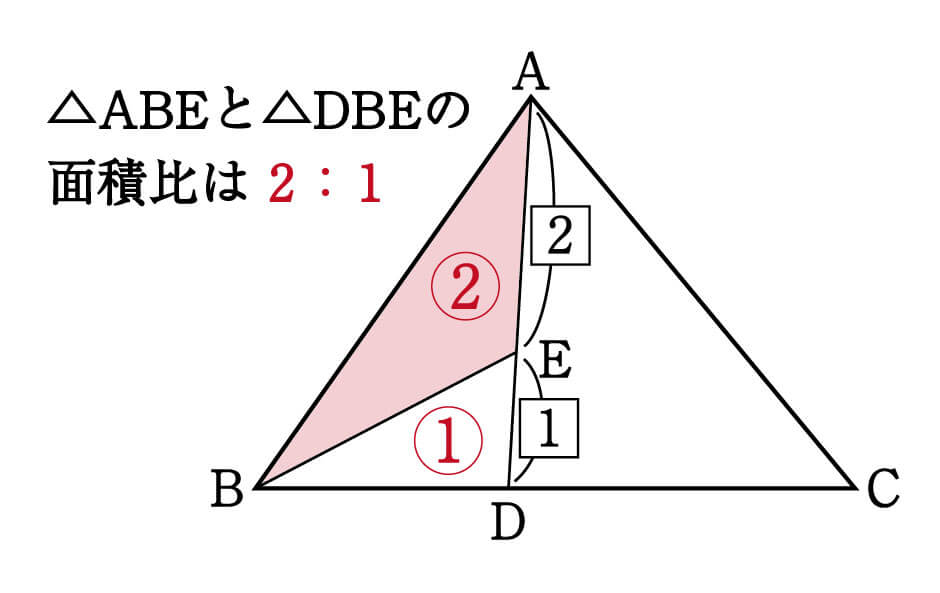
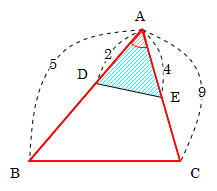
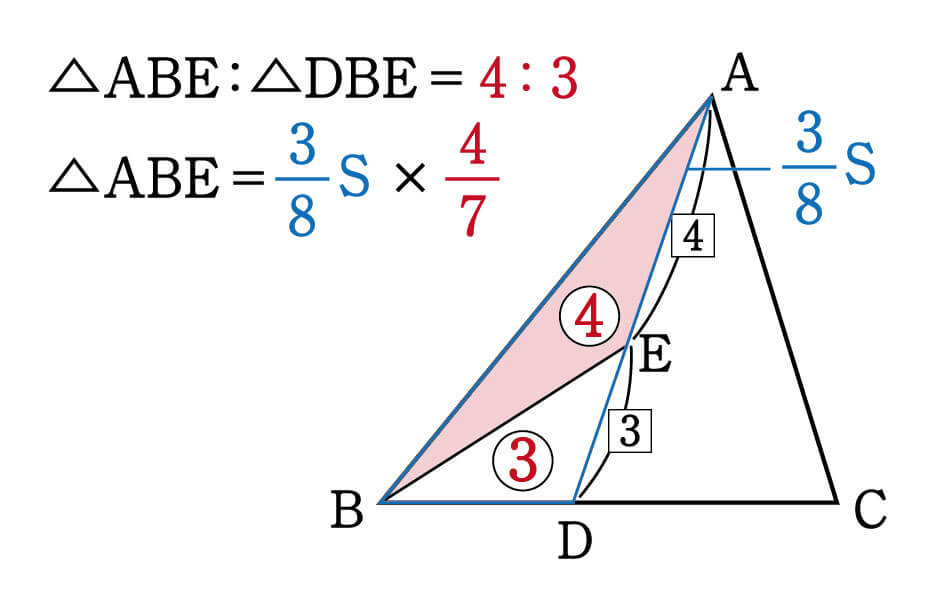
1つ目のステップでは、 ABDと ACDの面積比に注目します。 隣り合う三角形の①の型なので、底辺の比=3:5から面積比も3:5。 そして左側の ABDは、 ABCを8等分したうちの3つ分ですから、\( ABD\)の面積=\(\displaystyle \frac{3}{8}S\)と表すことができます。となり,1つの角を共有する2つの三角形の面積比は,その共有する角をはさむ2辺の積の比と等しくなります。 例題 無料動画講義(理論) 演習問題 無料動画講義(演習) 等高な三角形の面積比 補角をなす三角形の面積比 このページの学習内容でわからないところがある方縦横比は 。 数字が1減るに従い面積は2倍・辺長は 倍になる。 これらはA列以外でも多くの標準に共通である。 A0の面積は1m 2 である。 つまりmで表した縦横の辺長は互いに逆数になっており、 / である。 An判の丸めをしたサイズ(長辺)は次の式で得られる。 短辺はnを1増やせば得られる。




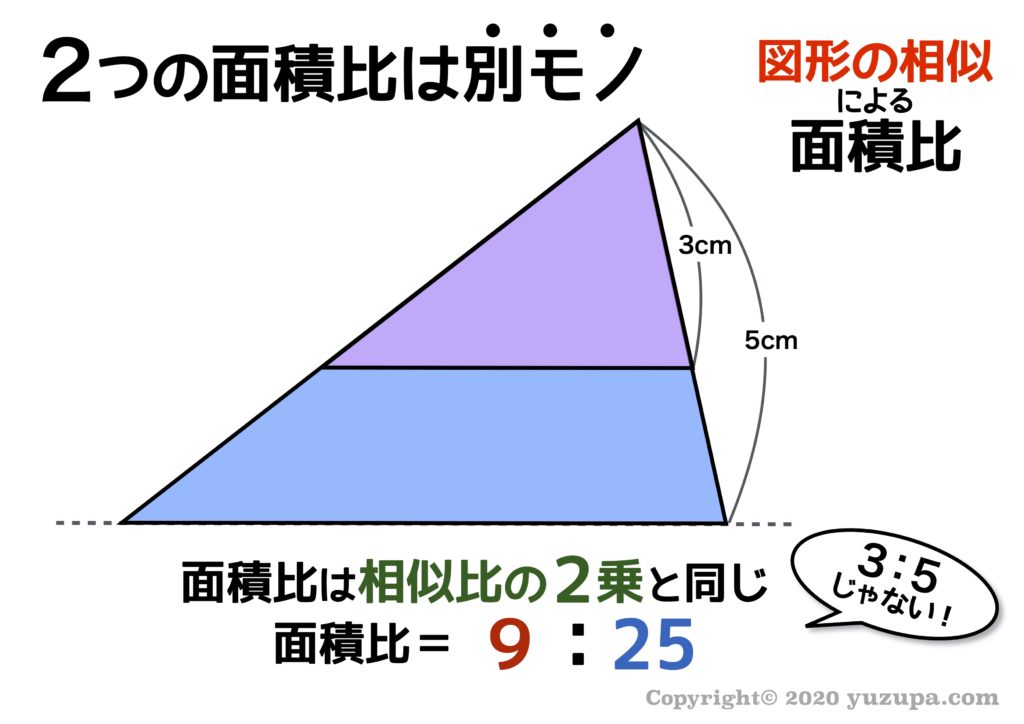
相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




相似比と面積比 中学3年数学 Youtube
面積比、長さ比の基本問題(学習院中等科 11年) 覚えておきたい白百合の三角形(1992年 白百合学園中学) 第10回算数オリンピック、ファイナルより→難問に挑戦! 立てた棒の影から長さを計算する(田園調布学園中等部 11年) 今年の名作問題ですSdr 界面の展開面積比 定義領域の展開面積(表面積)が、定義領域の面積に対してどれだけ増大しているかを表します。 完全に平坦な面のSdrは0となります。 表面に傾斜があるとSdrは大きくなります。 下の表面は45°の傾斜成分からなる平面ですが、Sdrは0414になります。(40%強、表面積が増えてい図2 2 2つの三角形の底辺の長さが等しいときは,面積の比は高さの比に等しい. 3 高さが書いていないときでも,1組の辺の比が mn のときは,高さが mn と考えてよい. 2の証明 三角形の面積は(底辺)×(高さ)÷2で求められる.右図の FBC と ABC の面積



面積比 長さ比 これが中学入試に出た図形問題



面積比 長さ比 中学受験ー算数解き方ポータル
相似比とは、辺の長さの比でした。それでは面積や体積の比はどうなるのでしょうか。 相似比がabのとき 面積比=(a×a)(b×b) 体積比=(a×a×a)(b×b×b) 例えば長方形の面積は「たて×横」なので、たての長さも横の長さも2倍になれば「2倍×2倍」に 面積比と線分比とチェバの定理 まずは、面積比ってなに? ってあなたは、こちらで理解しておいてほしいんじゃ おーい、ニャンコくん、面積比と線分比の関係についての解説記事をお願い! 数学にゃんこ はーい、先生! 面積比と線分比については > なぜ質量比と面積比がおなじになるのでしょう 図をご覧下さい。 解りやすくするために円ではなく四角で描きましたが、原理は同じです。 厚み(高さH)が同じで材質(比重ρ)が同じなら、重量比と面積比が同じになる事が直感的におわかりになると思いますが、いかがでしょう。 7;



辺の比と面積比




辺の比と面積比問題 考え方1 Youtube
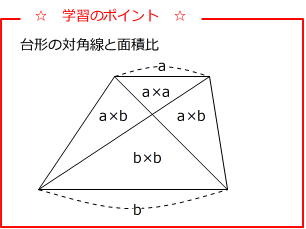
比べる三角形が相似でなくても、高さが等しければ 底辺の長さの比が、そのまま面積比となります。 問題を解いていく上で これら2つの特徴を利用していくことになるから しっかりと覚えておいてくださいね! 台形の面積比問題を解説相似比と面積比,体積比の公式の証明 レベル ★ 基礎 平面図形 更新日時 相似な平面図形について,面積比=相似比の二乗 相似な空間図形について,体積比=相似比の三乗 面積比をきちんと理解できれば体積比もほぼ同様に理解できるので なぜ面積比が上底と下底の \(2\) 乗になるかというと、\(2\) つの三角形が相似であるから、 高さの比も \((\text{上底}) (\text{下底})\) であるため です。 性質④2 本の対角線がなす左右の三角形の面積が等しい
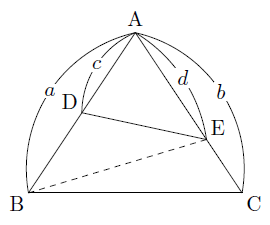



1角共有の三角形の面積比 まなびの学園
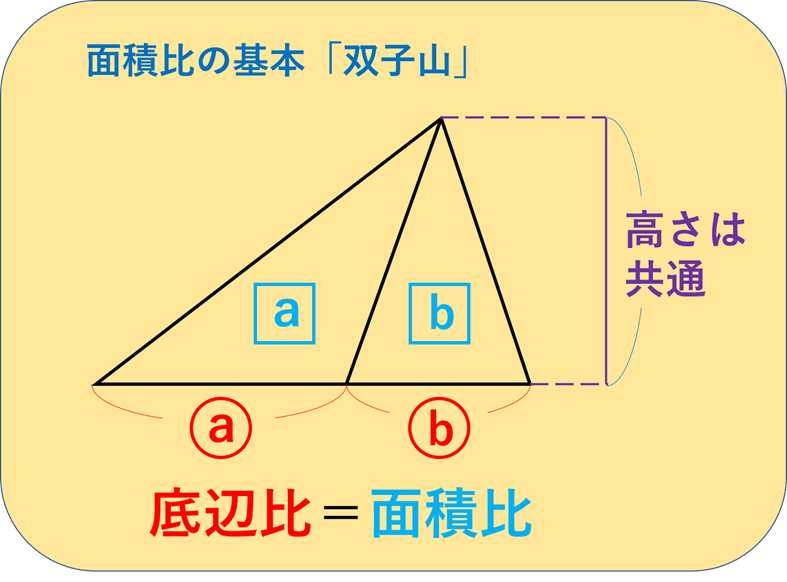



中学受験算数 平面図形 相似比と面積比の関係 中学受験プロ講師ブログ
面積比の基本問題です(学習院中等科 09年) 今年、13年の灘中学 2日目の問題(灘中学 13年) 正方形内の小さな円(浅野中学 10年) 今年、13年の問題→相似と面積比(開成中学 13年) 面積比、長さ比の基本問題(学習院中等科 11年) 覚えて海城中三角形の面積比 21年 21年 6年生 入試解説 東京 男子校 面積比 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に是非ご活用下さい。面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h Pの底面の半径を2rとするとQの底面の半径は3r Pの高さを2hとするとQの高さは3h ①表面積



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor
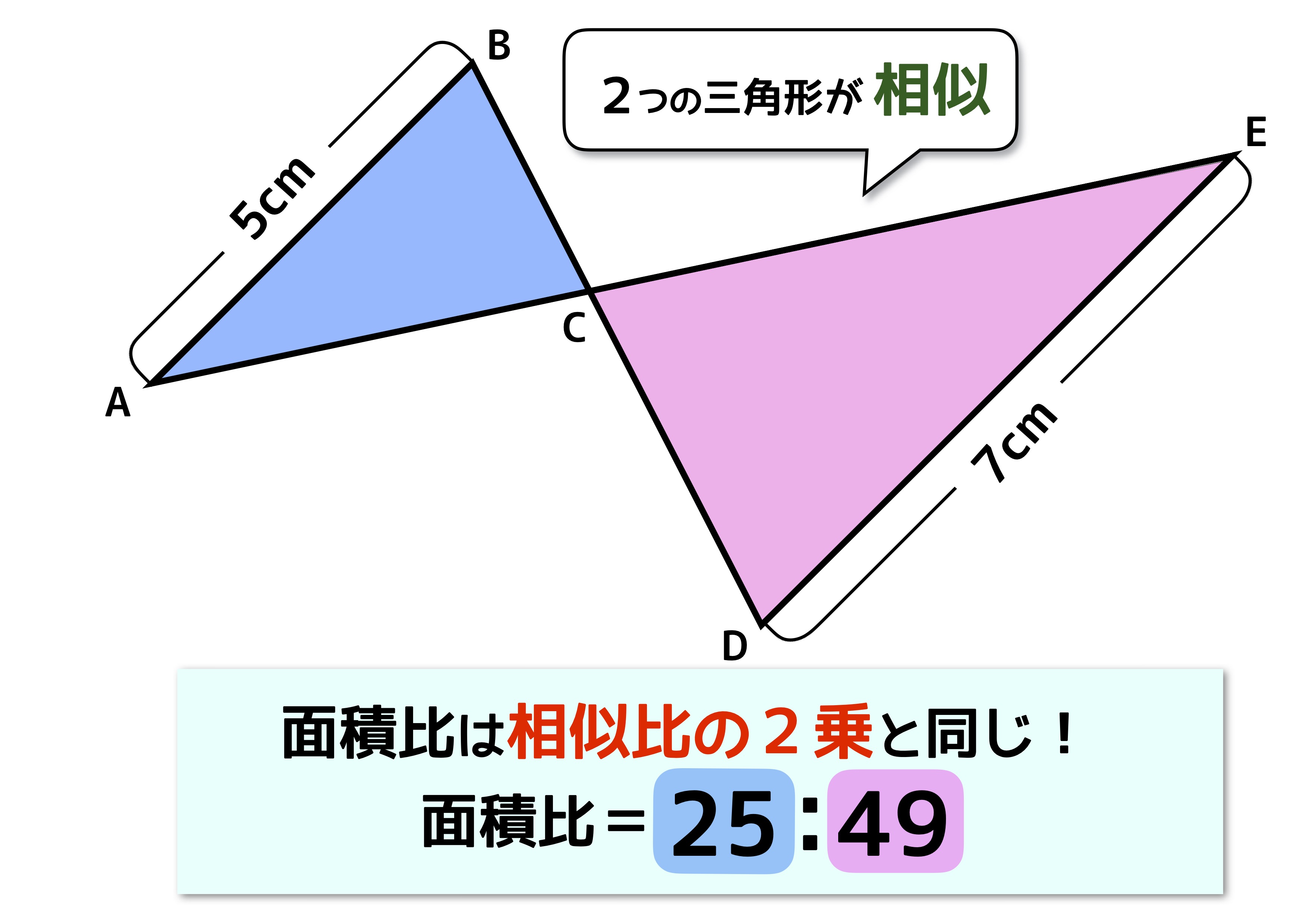



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
数学。三角形の面積比、この三角形の面積は全体の何分のいくつ? 数学。分数の中に分数がある場合の計算の方法。 カテゴリー プロフィール (1) やる気を出す方法 (4) 定期テスト (27) 高校受験 (38) おすすめ教材 (5) 人気記事 「単願」「併願」とは?私立高校入試の仕組み。 数学。分数の画像全体の面積(ピクセル数)である。(今回のSはピクセル) (8) T/Sが被覆率となる。 粒子径分布の解析 2値化した画像を利用して、粒子数のカウントや粒子サイズ分布を求めることができます。 (1) Analyze > Analyze Particlesを選択する。面積比と聞かれたら、何でもかんでも2乗して面積比を作っちゃう人がいるので気を付けてくださいね。 2乗が使えるのは相似な図形のときだけ! 上の問題のように、同じ高さの三角形では底辺の比がそのまま面積比となるのでしっかりと覚えておきましょう! 基礎編についてはこちらの動画で




平面図形をマスター 三角形の面積比 応用編その3



相似比とは 1分でわかる意味 面積比 四角形と三角形の問題
2 2つの三角形の底辺の長さが等しいときは,面積の比は高さの比に等しい. 3 高さが書いていないときでも,1組の辺の比が mn のときは,高さが mn と考えてよい. 2の証明 三角形の面積は(底辺)×(高さ)÷2で求められる.図3の fbc と abc の面積は各々 fbc = abc = ここで底辺 bc は共通だか「等高三角形の面積比(あるいは区切り面積)」 「隣辺比」 「相似の利用」 はその中でもよく出題される分野のひとつですから、 受講前の準備(既習範囲の知識の確認)、 受講後の復習(解法の習得と使い分け方)に取り組んで 、 「辺の比と面積比の問題はバッチリ!」 といえるように 全体の図形の面積の 何分のいくつでしょうか? 」 という問題を解くコツについて、 お話をしていきます。 今回のお話は 三角形の面積比を使用しますが、 三角形の面積比の求め方には 高さが同じ三角形の場合や




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう
全体の面積×キュウリの比をすれば答えが出る。 360×5/12=150 150㎡ トマトの面積は 全体の面積からキュウリの面積を引いた残りになる。 360―150=210 210㎡ 面積が60㎡と80㎡の2つの花壇の草取りを、生徒28人でします。広さの割合で分かれるとすると、何人と




高校入試file 003 数学 平面図形 三角形の面積比 ポイントは メネラウスの定理 Youtube



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



長さ比から面積比の求め方 算数解法の極意



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ



第416回 平面図形 の勉強方法 4 前田昌宏の中学受験が楽しくなる算数塾




平面図形の苦手を解消 三角形の面積比 基本編




大至急です 相似 面積比の問題です Clear



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



相似比と面積比と体積比はお友だち 苦手な数学を簡単に




面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




平面図形の苦手を解消 三角形の面積比 基本編



1



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



三角形の辺と面積の比 父ちゃんが教えたるっ



面積比




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




平面図形をマスター 三角形の面積比 応用編その3



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




よく出る台形の面積比 算数 過去問で基本を鍛える 12 勉強法のバイブル 帝都大学へのビジョン




相似じゃない三角形の面積比の求め方がよく分かりません Clear
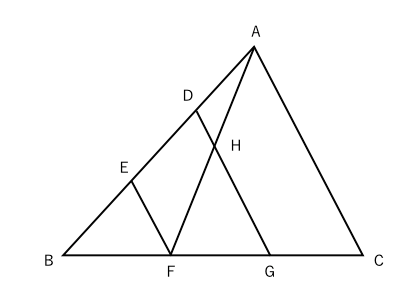



面積が何倍かを求める問題 応用編 苦手な数学を簡単に



三角形の面積比の求め方 算数解法の極意
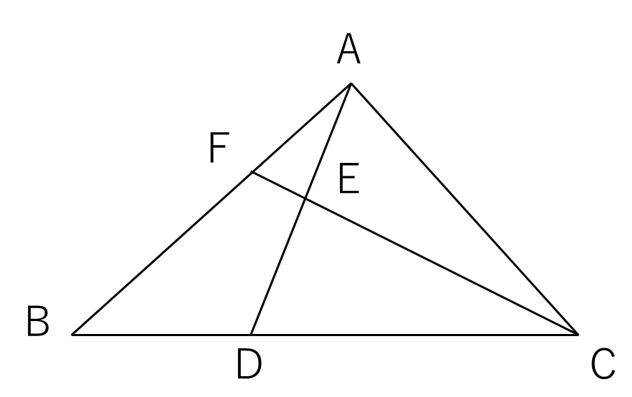



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ
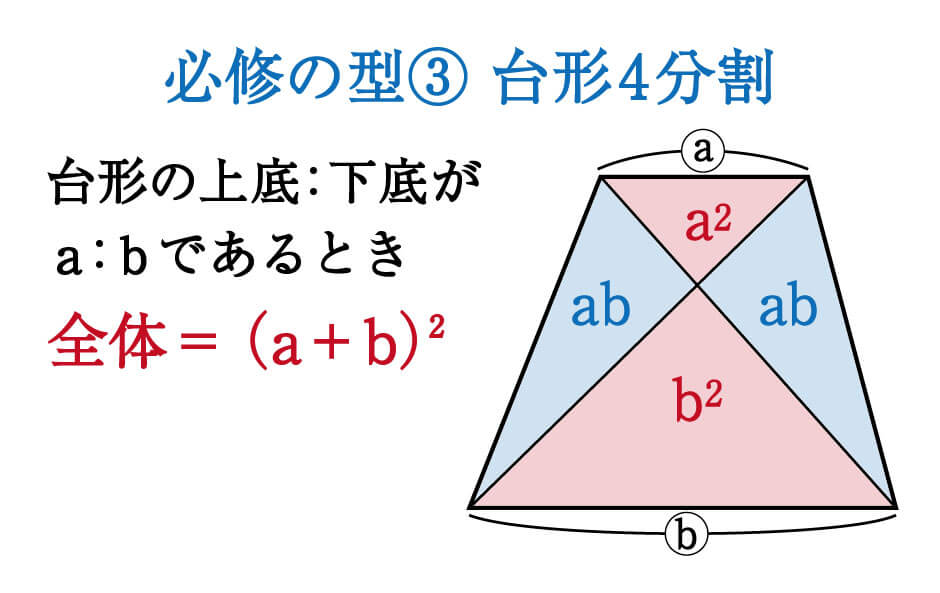



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
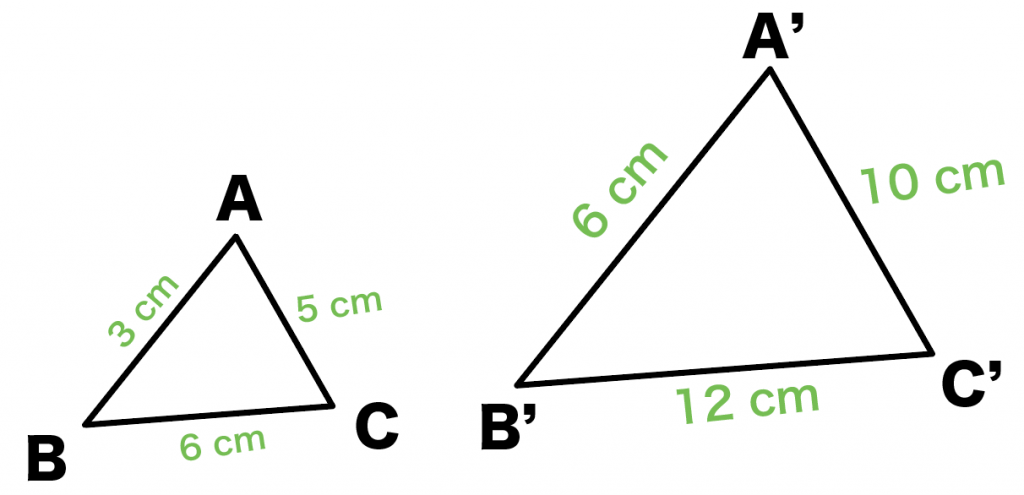



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
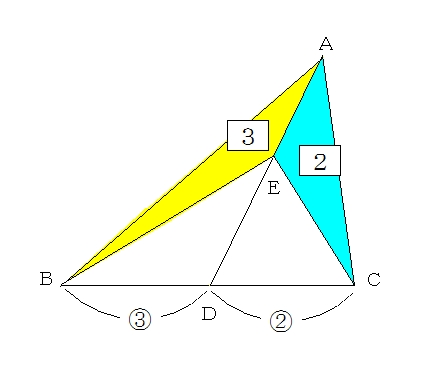



辺の比と面積比



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ
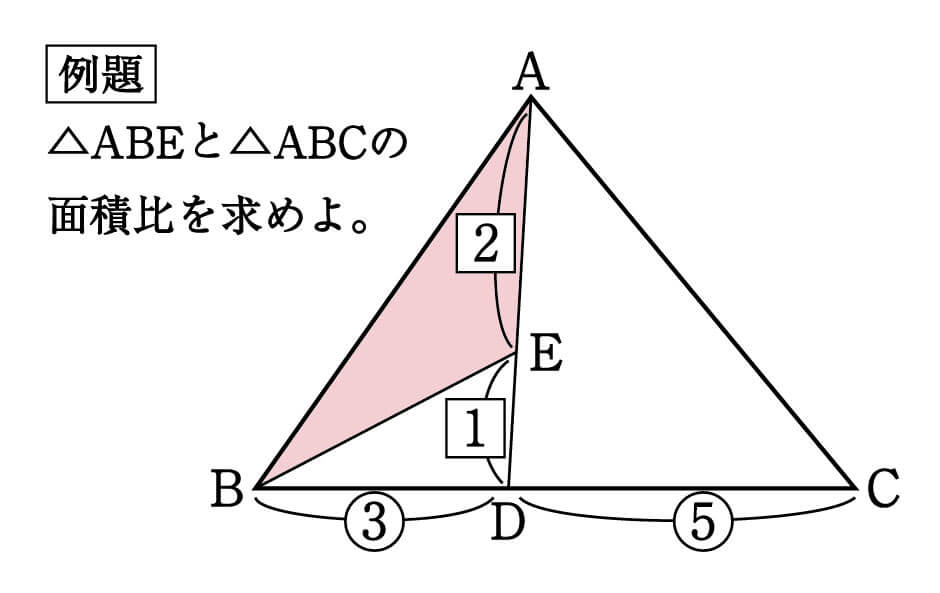



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の面積と面積比 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
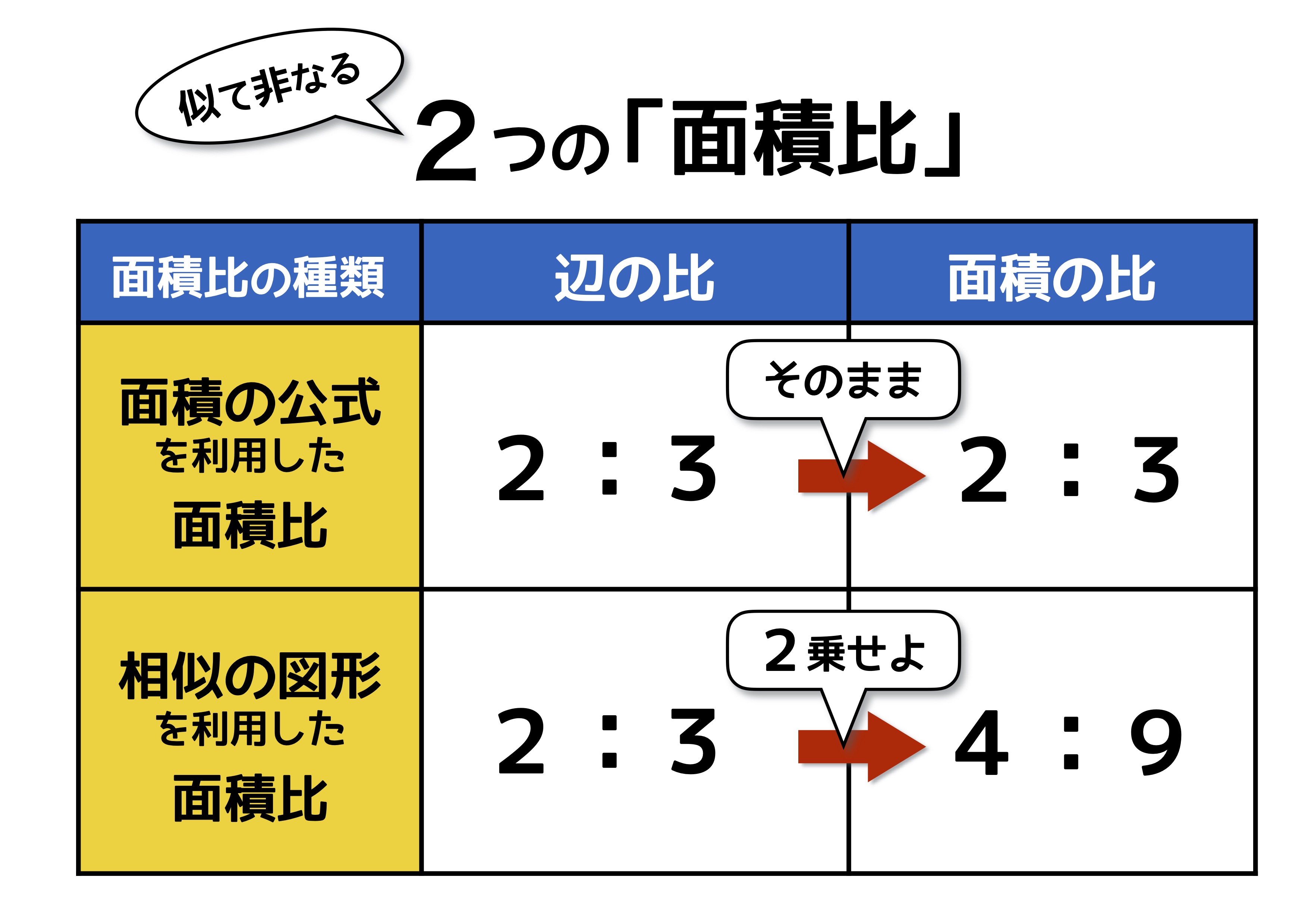



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
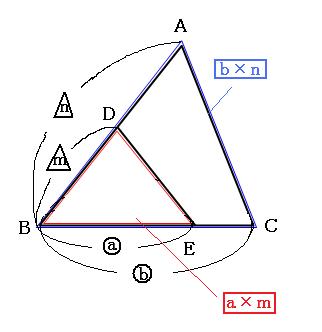



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める



相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1




これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ
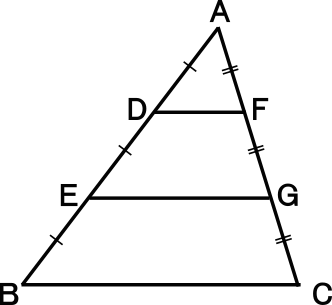



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似
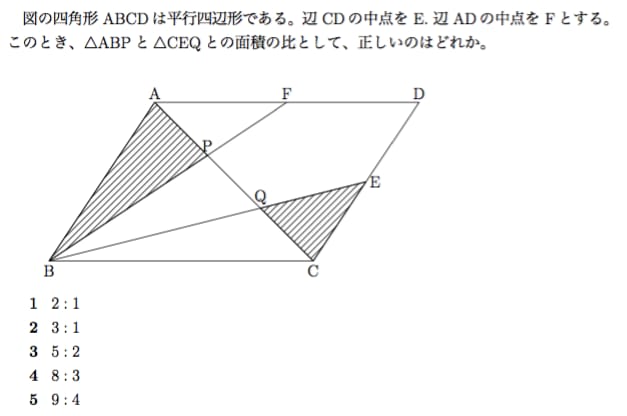



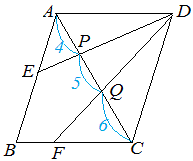
平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




平面図形をマスター 三角形の面積比 応用編その3



三角形の辺と面積の比 父ちゃんが教えたるっ
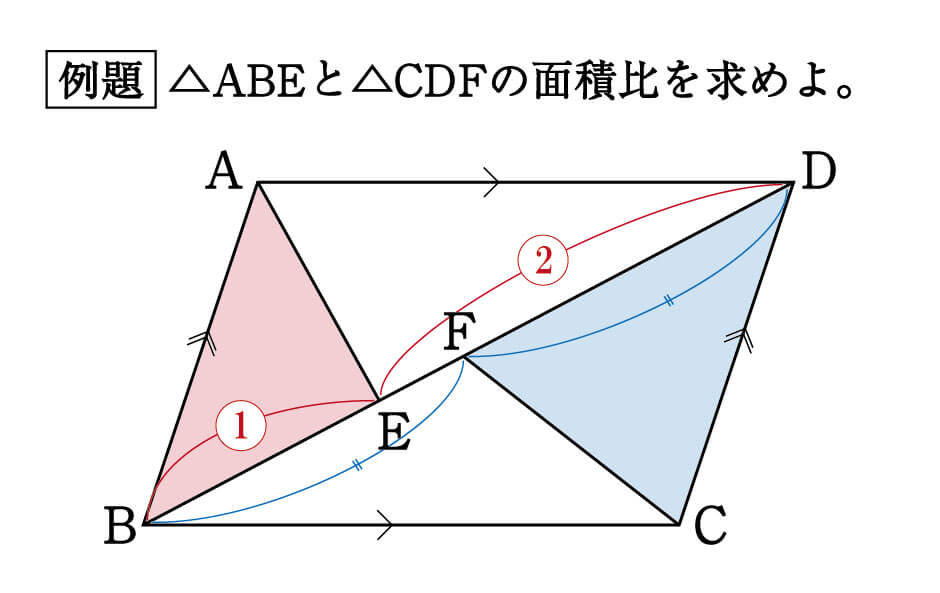



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
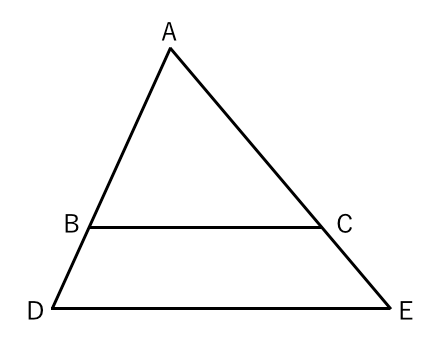



相似な図形 面積の比 苦手な数学を簡単に



1




平面図形をマスター 三角形の面積比 応用編その3




高校入試対策数学 面積比に関する対策問題 Pikuu




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



相似比と面積比 体積比の公式の証明 高校数学の美しい物語




辺の比と面積比 基本編 Youtube




中学受験算数 面積比の達人 仮 Yell Books みかん 本 通販 Amazon




三角形の面積比 数学の偏差値を上げて合格を目指す



第415回 平面図形 の勉強方法 3 前田昌宏の中学受験が楽しくなる算数塾



第5章 面積の比と体積の比 台形の相似比と面積比 中学生




平面図形をマスター 三角形の面積比 応用編その3




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




平面図形をマスター 三角形の面積比 応用編その3




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ
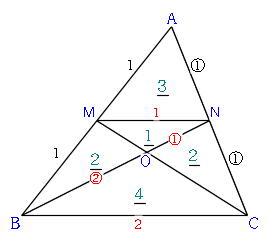



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ
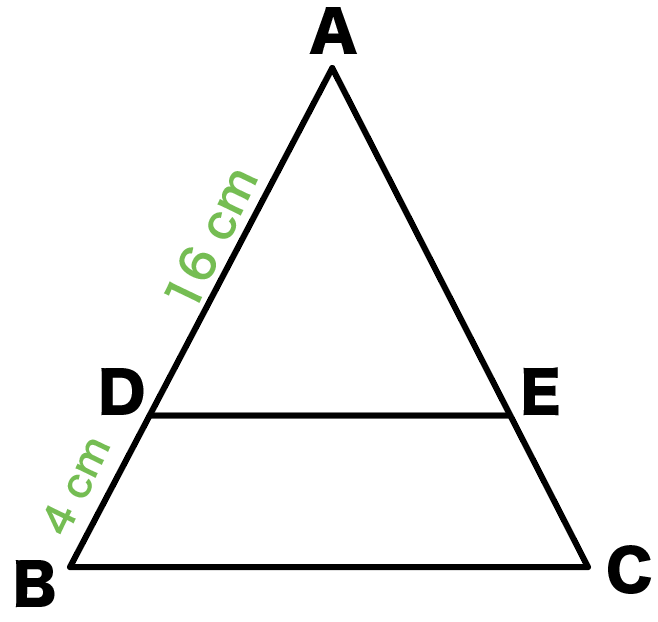



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




裏技 ベクトルと面積比 これ知らない奴来い Youtube
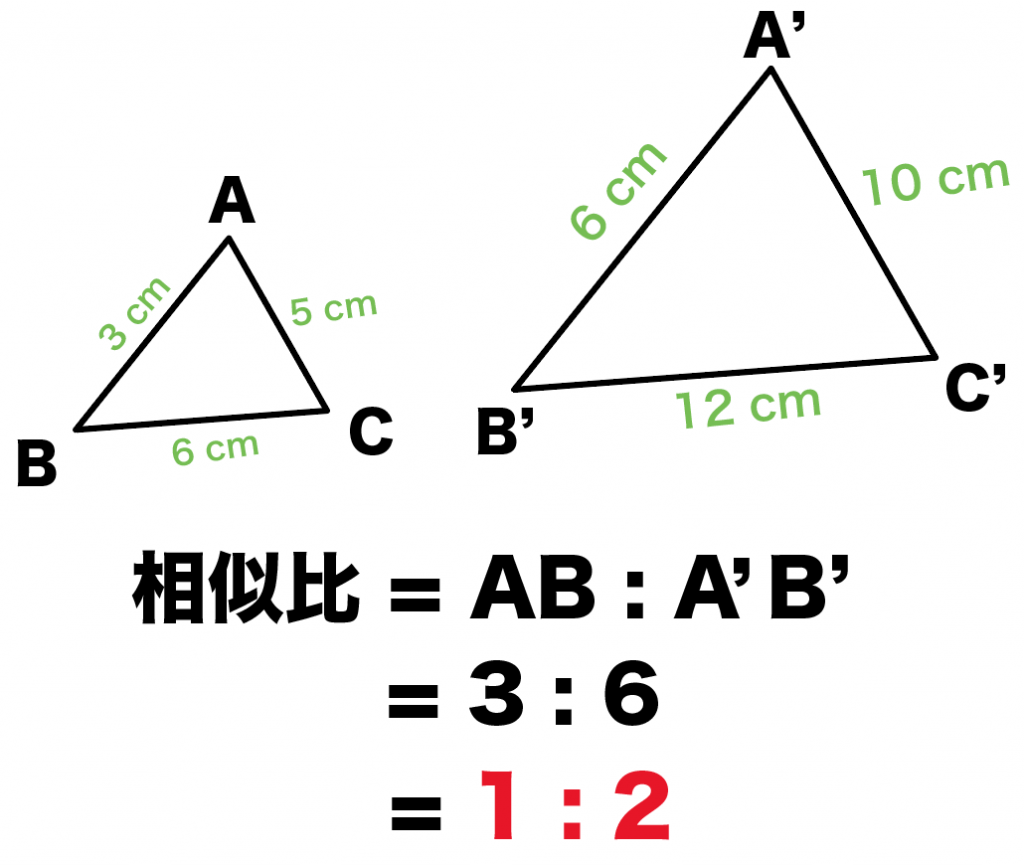



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中3 20 1 線分比と面積比 1 Youtube




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生
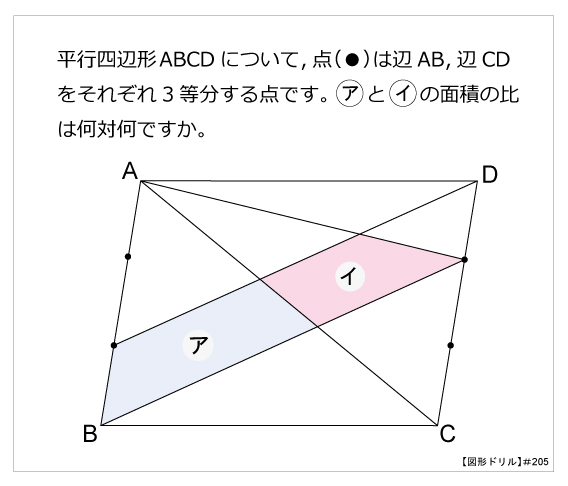



図形ドリル 第5問 平行四辺形内の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ




平面図形の苦手を解消 三角形の面積比 基本編
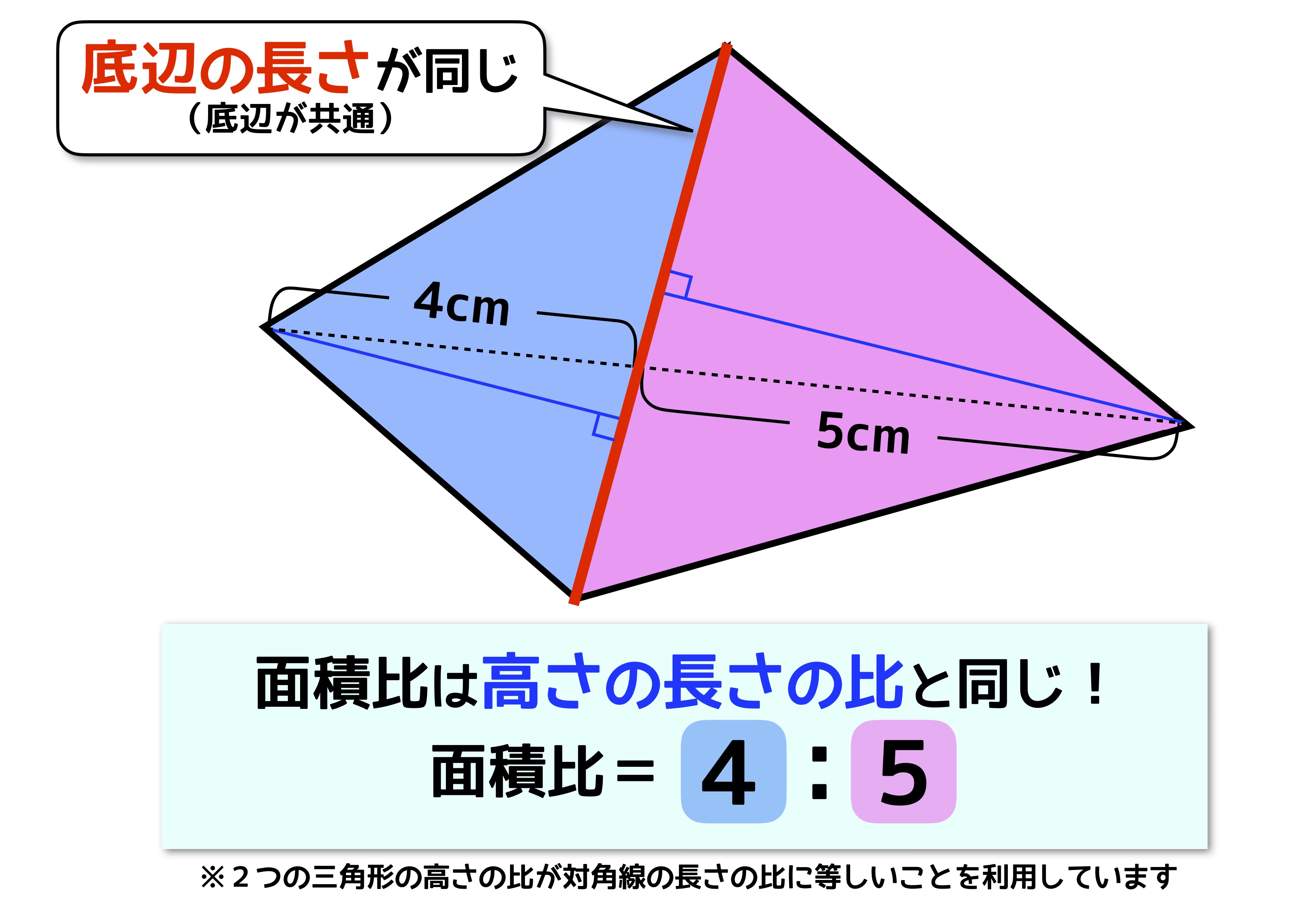



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
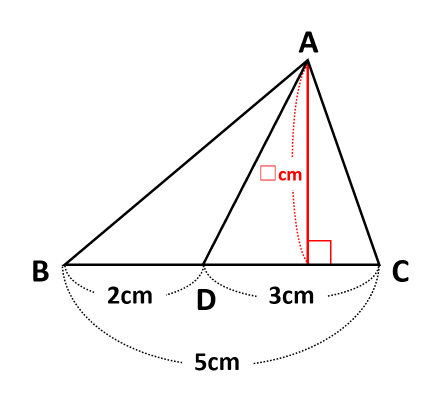



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



3
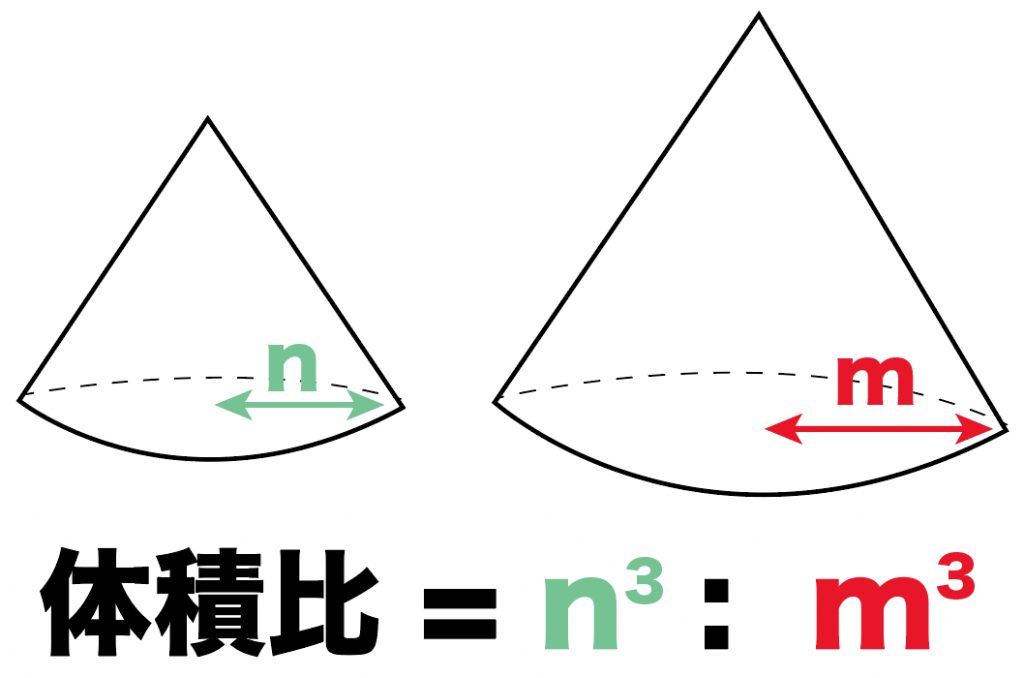



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室
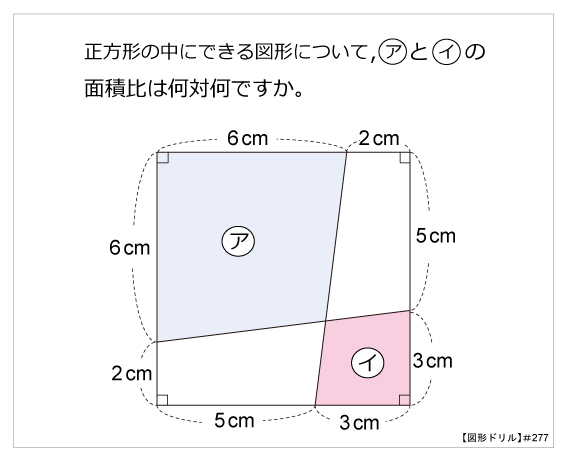



図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
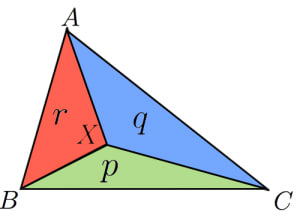



ベクトルの定番問題を一瞬で解く公式 高校数学の美しい物語




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 暇つぶしに動画で脳トレ



0 件のコメント:
コメントを投稿